filmov
tv
_-substitution: definite integral of exponential function | AP Calculus AB | Khan Academy

Показать описание
Finding the definite integral from 0 to 1 of x__2^(x_). Created by Sal Khan.
AP Calculus AB on Khan Academy: Bill Scott uses Khan Academy to teach AP Calculus at Phillips Academy in Andover, Massachusetts, and heÕs part of the teaching team that helped develop Khan AcademyÕs AP lessons. Phillips Academy was one of the first schools to teach AP nearly 60 years ago.
For free. For everyone. Forever. #YouCanLearnAnything
_-substitution: definite integral of exponential function | AP Calculus AB | Khan Academy
Integrating Exponential Functions By Substitution - Antiderivatives - Calculus
Integration by Substitution: Definite Integral with an Exponential Function
Definite Exponential Integration with Substitution
Example: Definite Integral by Substitution (Exponential)
How to Evaluate a Definite Integral with U-Substitution (Example with Exponential and Trig Function)
Learn How to Evaluate a Definite Integral with a u substitution (Exponential with Base 5 Example)
U-substitution With Definite Integrals
INTEGRAL (PART-5) | NCERT | MATHS | CLASS 12TH | BOARD EXAM 2024-2025
How to find the integral of an exponential function using u sub
How to integrate exponential expression with u substitution
_-substitution: definite integrals | AP Calculus AB | Khan Academy
Integrate exponential function using substitution method | Tutorial 4 | Q4
Ex: Indefinite Integral Using Substitution with Exponential and Sine
Integrating Exponential Functions with Substitution | Calculus 1 Exercises
AS/A-Level Maths Integration - Integration of Exponential functions (using Substitution)
Integration by Substitution: Indefinite Integral with Exponential Functions
u-Substitution with Exponential Integrals
Integration by Substitution Exponentials
Evaluate a Definite Integral Involving an Exponential Function (Not Base e)
Basic Integration Example 06 (To Substitute or Not ~ Exponential)
Math Integral Calculus - u substitution definite integral of exponential function
Evaluating the integral with exponential and u sub
Integrate exponential function using substitution method | Tutorial 4 | Q5
Комментарии
 0:07:53
0:07:53
 0:11:16
0:11:16
 0:08:21
0:08:21
 0:10:07
0:10:07
 0:03:02
0:03:02
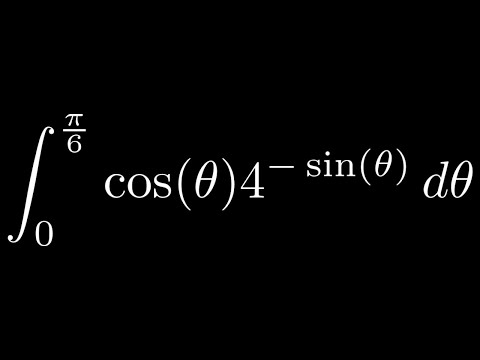 0:04:32
0:04:32
 0:04:14
0:04:14
 0:11:03
0:11:03
 0:33:15
0:33:15
 0:01:04
0:01:04
 0:01:20
0:01:20
 0:05:53
0:05:53
 0:02:18
0:02:18
 0:02:32
0:02:32
 0:16:32
0:16:32
 0:16:38
0:16:38
 0:09:27
0:09:27
 0:05:19
0:05:19
 0:22:55
0:22:55
 0:03:13
0:03:13
 0:03:37
0:03:37
 0:07:53
0:07:53
 0:01:07
0:01:07
 0:03:29
0:03:29