filmov
tv
Integral test for Series
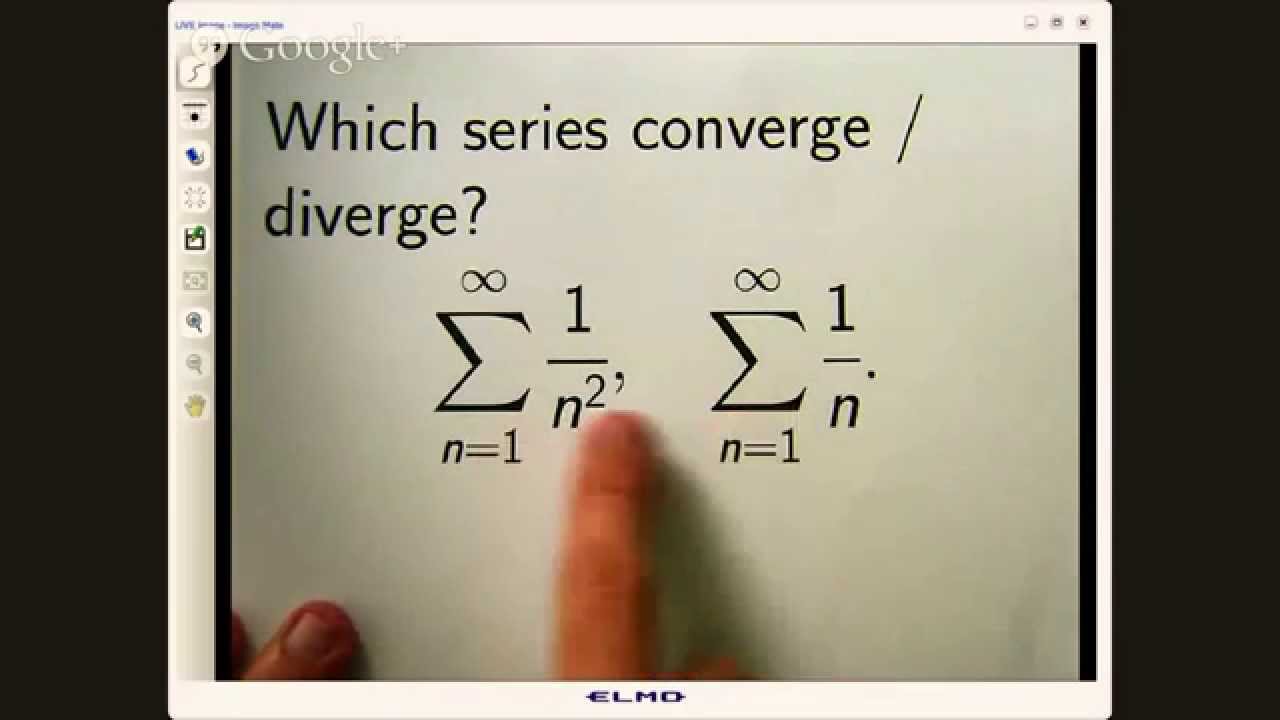
Показать описание
Consider an integer N and a non-negative function f defined on the unbounded interval [N, ∞), on which it is monotone decreasing. Then the infinite series
\sum_{n=N}^\infty f(n)
converges to a real number if and only if the improper integral
\int_N^\infty f(x)\,dx
is finite. In other words, if the integral diverges, then the series diverges as well.
\sum_{n=N}^\infty f(n)
converges to a real number if and only if the improper integral
\int_N^\infty f(x)\,dx
is finite. In other words, if the integral diverges, then the series diverges as well.
0:28:17
Calculus 2 - Integral Test For Convergence and Divergence of Series
0:08:46
Integral test | Series | AP Calculus BC | Khan Academy
0:08:55
Integral Test | Derivation & 1st Example
1:11:52
Calculus 2 Lecture 9.3: Using the Integral Test for Convergence/Divergence of Series, P-Series
0:09:56
Estimating Sums Using the Integral Test and Comparison Test
0:09:05
Worked example: Integral test | Series | AP Calculus BC | Khan Academy
0:05:49
Calculus, Integral Test, 11 3 #26
0:08:20
Using the Integral Test for Series
1:36:20
Week 13 review problems for Calculus 1 (Fall 2024)
0:44:13
Integral Test For Series | Calculus 2 Lesson 23 - JK Math
0:20:28
11.3 Integral test | Anas Abu Zahra
0:08:39
Integral Test for Series
0:08:31
How To Use The Integral Test For Infinite Series
0:14:47
Integral Test for Series: Why It Works
0:43:52
Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test
0:38:18
Integral Test For Series Examples | Calculus 2 - JK Math
0:13:43
Calculus II - 9.3.1 The Integral Test
0:13:20
Infinite Series - Cauchy's Integral Test For Convergence of Series
0:09:41
The Integral Test
0:26:56
P-Series & Integral Test, Calculus 2
0:09:03
Estimating the Remainder of a Series Approximation via the Integral Test
0:11:16
How to use the INTEGRAL TEST for series
0:35:34
Calculus 2: The Integral Test (Section 11.3) | Math with Professor V
0:38:12
Calculus 2 ( Ch11 ) series : Integral Test
Комментарии