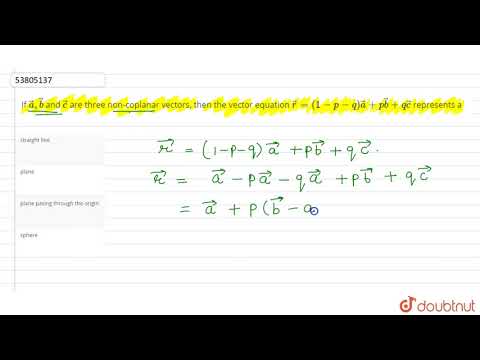
If `veca, vecb` and `vecc` are unit coplanar vectors, then the scalar triple product `[(2v

preview_player
Показать описание
If `veca, vecb` and `vecc` are unit coplanar vectors, then the scalar triple product `[(2veca-vecb, 2vecb-vecc, 2vecc-veca)]=`
  1. Doubtnut
Рекомендации по теме
If `vecA, vecB` 0:05:18

If `vecA, vecB` and `vecC` are vectors such that `|vecB|=|C|` Provethat `[(vecA+ vecB)× (vec

If ` veca. 0:05:56

If ` veca. Vecb and vecc` are unit vectors satisfying ` |veca -vecb|^(2) +|vecb -vecc|

If `vecA = 0:02:59

If `vecA = vecB + vecC` and the magnitudes of `vecA, vecB and vecC` a een `vecA` and `vecC` is :

If `vecA,vecB` and 0:04:24

If `vecA,vecB` and `vecC` are coplanar vectors, then

If `veca, vecb` 0:03:52

If `veca, vecb` and `vecc` are vectors such that `vecb` and `vecc` are perpendicular, but `vec

If `veca,vecb and 0:06:22

If `veca,vecb and vecc ` are vectors such that `|vecb|=|vecc|` then `{(veca+vecb)xx(veca+vecc)}xx

If veca, vecb 0:02:53

If veca, vecb and vecc are three unit vectors such that veca xx (vecb xx vecc) = 1/2 vecb , then...

If `veca, vecb` 0:06:46

If `veca, vecb` and `vecc` are three non co planar vectors, then the length of projection of v

If `veca, vecb 0:04:27

If `veca, vecb and vecc` are vectors such that `|veca|=3,|vecb|=4 and |vec|=5 and (veca+vecb)` is

If `veca,vecb` and 0:01:41

If `veca,vecb` and `vecc` are three non-coplanar vectors, then the vector equation

If veca, vecb 0:04:30

If veca, vecb and vecc are such that [veca vecb vecc] =1, vecc= lambda veca xx vecb, angle betwe...

If veca, vecb 0:04:02

If veca, vecb and vecc are three unit vectors such that veca xx (vecb xx vecc) = 1/2 vecb , then...

If `vecA,vecB and 0:05:15

If `vecA,vecB and vecC` are three non coplanar then `(vecA+vecB+vecC).{(vecA+vecB)xx(vecA+vecC)}

If `veca,vecb` and 0:03:41

If `veca,vecb` and `vec c` are perpendicular to `vecb+vecc, vecc+veca, veca+vecb` respectively ...

If `veca, vecb 0:03:31

If `veca, vecb and vecc ` are unit vectors then `|veca-vecb|^2+|vecb-vecc|^2+|vecc-veca|^2` i

If veca , 0:04:30

If veca , vecb and vecc are three vectors such that vecaxx vecb =vecc, vecb xx vecc= veca, vecc...

Theorem 2: If 0:04:59

Theorem 2: If `veca`, `vecb` and `vecc` are non coplanar vectors; then any vector `vecr` can be

If `veca,vecb and 0:02:31

If `veca,vecb and vecc` are non coplanar and unit vectors such that `vecaxx(vecbxxvecc)=(vecb+vecc)

If `veca,vecb and 0:02:48

If `veca,vecb and vecc` are non coplaner vectors such that `vecbxxvecc=veca`, `veccxxveca=vecb

If `veca,vecb and 0:06:46

If `veca,vecb and vecc` are non coplnar and non zero vectors and `vecr` is any vector in space then`

If `veca, vecb` 0:02:52

If `veca, vecb` and `vecc` are unit coplanar vectors, then the scalar triple product `[(2v

If veca ,vecb 0:03:30

If veca ,vecb and vecc are three mutually orthogonal unit vectors , then the triple product [vec...

If `veca,vecb and 0:10:17

If `veca,vecb and vecc` are three non coplanar vectors and `vecr` is any vector in space, then

If the three 0:04:17

If the three vectors `veca,vecb,vecc` are such that `veca+vecb+vecc=vec0' and