filmov
tv
Implicit Differentiation: Practice 5 - Thinking about it from another perspective (Calculus 1)
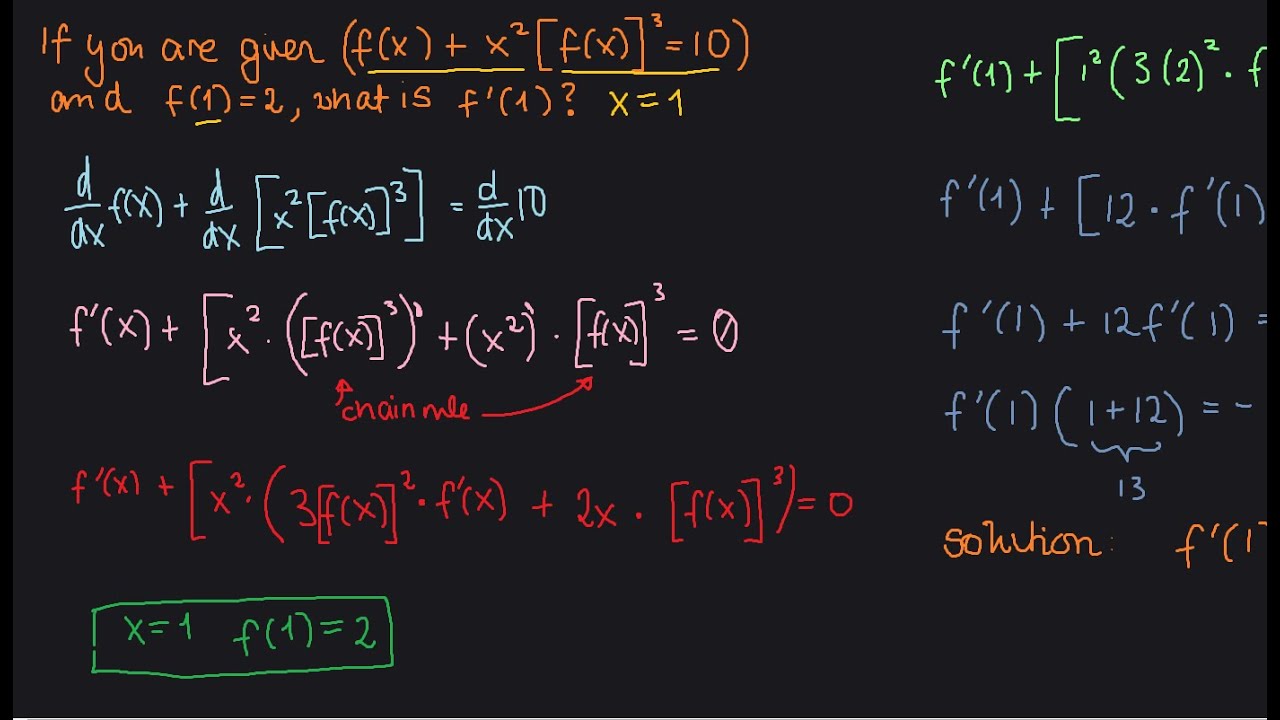
Показать описание
Summary:
The video is a tutorial on practicing implicit differentiation with a unique equation. The instructor focuses on finding f`(1) when the equation f(x)+x^2[f(x)]^3=10, and f(1)=2 are given.
The differentiation process involves the chain rule, product rule, and simplification techniques. The instructor emphasizes the steps involved in implicit differentiation. By the end of the video, the instructor derives that f´(1)= -16/13.
Table of Contents with Times:
0:00 - Introduction to the topic and the equation to be differentiated.
1:20 - Explanation of the given equation and the goal of the tutorial.
2:40 - Differentiating the equation implicitly.
4:00 - Applying the chain rule and product rule.
5:30 - Simplifying the differentiated equation.
6:45 - Plugging in the given values and solving for f´(1).
7:30 - Final solution: -16/13
The video is a tutorial on practicing implicit differentiation with a unique equation. The instructor focuses on finding f`(1) when the equation f(x)+x^2[f(x)]^3=10, and f(1)=2 are given.
The differentiation process involves the chain rule, product rule, and simplification techniques. The instructor emphasizes the steps involved in implicit differentiation. By the end of the video, the instructor derives that f´(1)= -16/13.
Table of Contents with Times:
0:00 - Introduction to the topic and the equation to be differentiated.
1:20 - Explanation of the given equation and the goal of the tutorial.
2:40 - Differentiating the equation implicitly.
4:00 - Applying the chain rule and product rule.
5:30 - Simplifying the differentiated equation.
6:45 - Plugging in the given values and solving for f´(1).
7:30 - Final solution: -16/13
 0:02:22
0:02:22
 0:07:57
0:07:57
 0:08:41
0:08:41
 0:14:34
0:14:34
 0:06:24
0:06:24
 0:08:41
0:08:41
 0:11:45
0:11:45
 0:04:57
0:04:57
 1:21:34
1:21:34
 0:18:10
0:18:10
 0:07:14
0:07:14
 0:08:01
0:08:01
 0:04:31
0:04:31
 0:03:51
0:03:51
 0:05:00
0:05:00
 0:06:27
0:06:27
 0:13:46
0:13:46
 0:30:33
0:30:33
 0:04:02
0:04:02
 0:33:32
0:33:32
 0:28:59
0:28:59
 0:12:16
0:12:16
 0:21:21
0:21:21
 0:23:37
0:23:37