filmov
tv
Solve any equation using gradient descent

Показать описание
Gradient descent is an optimization algorithm designed to minimize a function. In other words, it estimates where a function outputs its lowest value.
This video demonstrates how to use gradient descent to approximate a solution for the unsolvable equation x^5 + x = 3.
We seek a cubic polynomial approximation (ax^3 + bx^2 + cx + d) to cosine on the interval [0, π].
This video demonstrates how to use gradient descent to approximate a solution for the unsolvable equation x^5 + x = 3.
We seek a cubic polynomial approximation (ax^3 + bx^2 + cx + d) to cosine on the interval [0, π].
Solve any equation using gradient descent
Gradient of straight line
Finding the equation of a straight line given the gradient and a point
Intro to Gradient Descent || Optimizing High-Dimensional Equations
GCSE Maths - How to Find the Gradient of a Straight Line #65
Straight-Line Graphs: Find Gradient From Graph (m = Positive) (Grade 4) - GCSE Maths Revision
How to Calculate Gradient
Slope Intercept Form Y=mx+b | Algebra
Revision session Week 5 and 6
Gradient of a line
lines gradient and equation
GCSE Maths - What on Earth is y = mx + c #67
Calculating the Gradient of Straight Line using the formula|| How to calculate Gradient
Calculus Grade 12: Gradient is given
Grade 9 to 12: Gradient
Find gradient
| colourful liquid density gradient | layers of liquid in glass |Awesome science experiment
Finding Coordinates Given the Gradient (4/6 Calculus Video)
How To Calculate The Gradient of a Straight Line
NECO 2020 Question 22 | Gradient and y-intercept
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Algebra Basics: Slope And Distance - Math Antics
Linear Equations - Algebra
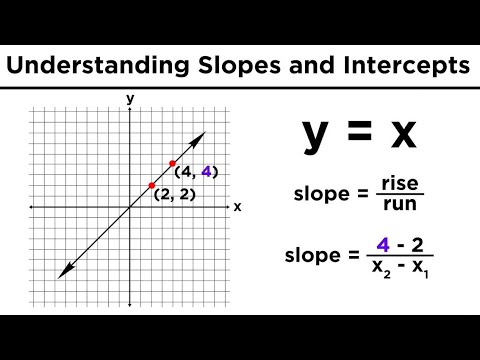
Graphing Lines in Algebra: Understanding Slopes and Y-Intercepts
Комментарии
 0:09:05
0:09:05
 0:00:15
0:00:15
 0:01:54
0:01:54
 0:11:04
0:11:04
 0:06:48
0:06:48
 0:00:54
0:00:54
 0:00:34
0:00:34
 0:08:39
0:08:39
 2:01:26
2:01:26
 0:00:47
0:00:47
 0:09:37
0:09:37
 0:04:53
0:04:53
 0:03:33
0:03:33
 0:00:57
0:00:57
 0:03:27
0:03:27
 0:00:09
0:00:09
 0:00:16
0:00:16
 0:08:28
0:08:28
 0:05:32
0:05:32
 0:03:12
0:03:12
 0:15:42
0:15:42
 0:12:00
0:12:00
 0:32:05
0:32:05
 0:06:52
0:06:52