filmov
tv
Integration durch Substitution - Verkettung || StrandMathe || Oberstufe ★ Übung 1

Показать описание
Integration durch Substitution - Verkettung
So wie die Produktintegration (partielle Integration) die Umkehrung zur Produktregel beim Ableiten ist, verhält sich die Substitution beim Integrieren entsprechend der Kettenregel. Das Substituieren (von lat. substituere, ‚ersetzen‘) lässt sich anwenden, wenn eine Funktionsverkettung f(g(x) ) vorliegt, die mit der Inneren Ableitung g^' (x) multipliziert wird. Man vereinfacht das Integral, indem man die Grenzen des Integrals als g(a) und g(b) ausdrückt und lediglich die Stammfunktion der reduzierten Form f(z) bestimmt.
Da es in diesem Kapitel um Substitution geht, kannst du direkt Ausschau nach einer „versteckten“ Teilfunktion g(x) und ihrer Ableitung g^' (x) halten. Das Vorgehen ist natürlich deutlich erschwert, wenn du erst herausfinden musst, ob eine Substitution in Frage kommt.
Wenn wir auf die Formel von oben blicken, dann sieht man, dass wir in dem Integral eine verschachtelte Teilfunktion g(x) finden müssen. Deine Erfahrung aus den vorangegangen Kapiteln führt dich vermutlich darauf, dass solche Teilfunktionen oft in einem Klammerausdruck oder im Nenner oder eben in beidem auftreten. Daher nehmen wir an:
Mit dieser Annahme überprüfst du nun, ob sich g'(x) als Faktor finden lässt, damit die Formel von oben erfüllt ist. Tatsächlich taucht dort 3x^2 als Faktor von f(g(x) ) auf. Um daraus das vereinfachte Integral zu bilden, wird die Funktion f(z) isoliert betrachtet:
Als Nächstes können wir das zu lösende Integral aufschreiben, die Grenzen verändern und die Stammfunktion bestimmen.
Auf diese Art und Weise kannst du das komplizierte Integral aus der Aufgabe lösen.
Trainer: „Bei schwierigen Integrationen solltest du immer durch Ableiten überprüfen, ob deine Stammfunktion richtig ist.“
 0:06:33
0:06:33
 0:10:49
0:10:49
 0:04:14
0:04:14
 0:07:23
0:07:23
 0:08:23
0:08:23
 0:06:05
0:06:05
 0:04:12
0:04:12
 0:06:36
0:06:36
 0:02:41
0:02:41
 0:05:41
0:05:41
 0:02:29
0:02:29
 0:07:50
0:07:50
 0:09:17
0:09:17
 0:07:38
0:07:38
 0:13:10
0:13:10
 0:07:31
0:07:31
 0:04:09
0:04:09
 0:05:32
0:05:32
 0:05:02
0:05:02
 0:09:15
0:09:15
 0:07:41
0:07:41
 0:10:28
0:10:28
 0:06:50
0:06:50
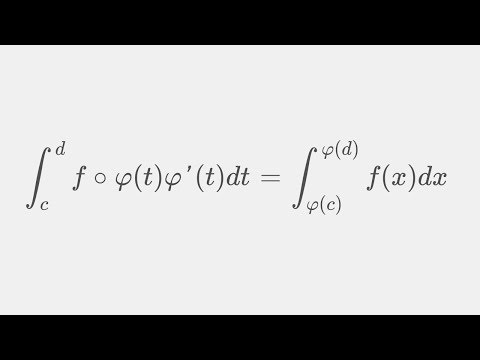 0:05:09
0:05:09