Douglas Arnold | Preserving geometry in numerical discretization

12/2/2020 Colloquium

Speaker: Douglas Arnold (U of Minnesota)

Title: Preserving geometry in numerical discretization

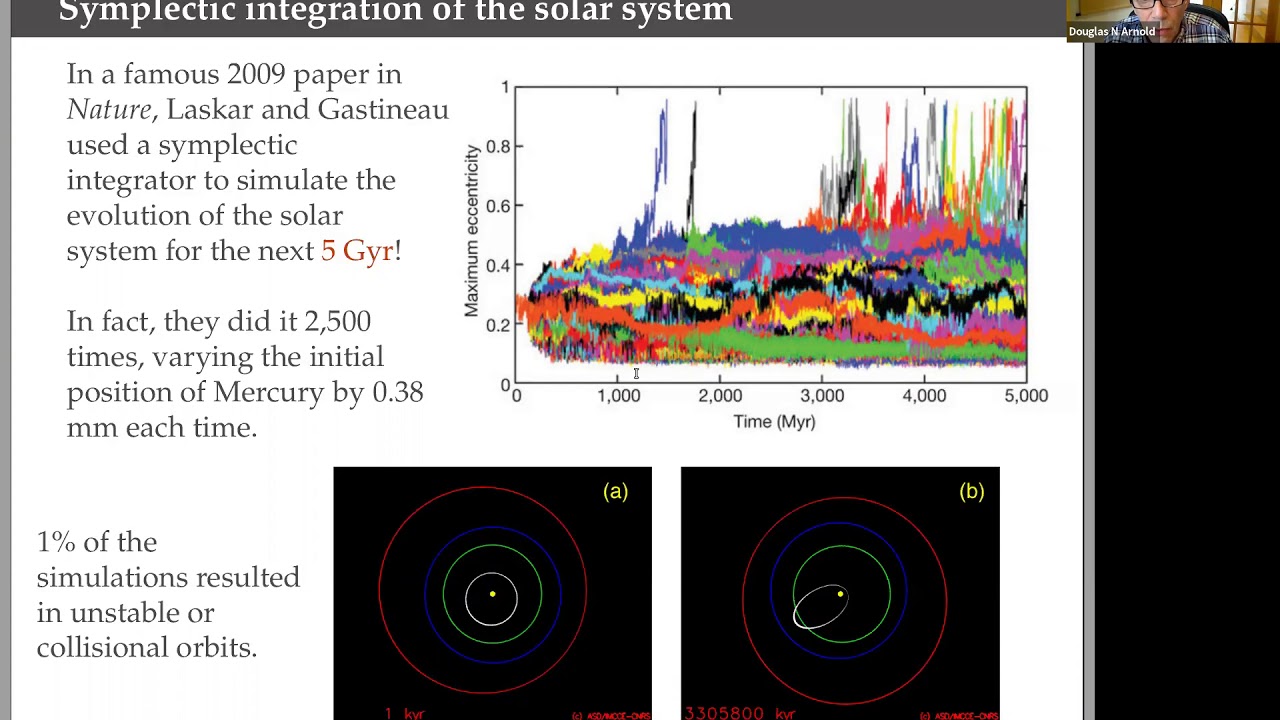
Abstract: An important design principle for numerical methods for differential equations is that the discretizations preserve key geometric, topological, and algebraic structures of the original differential system. For ordinary differential equations, such geometric integrators were developed at the end of the last century, enabling stunning computations in celestial mechanics and other applications that would have been impossible without them. Since then, structure-preserving discretizations have been developed for partial differential equations. One of the prime examples has been the finite element exterior calculus or FEEC, in which the structures to preserve are related to Hilbert complexes underlying the PDEs, the de Rham complex being a canonical example. FEEC has led to highly successful new numerical methods for problems in fluid mechanics, electromagnetism, and other applications which relate to the de Rham complex. More recently, new tools have been developed which extend the applications of FEEC far beyond the de Rham complex, leading to progress in discretizations of problems from solid mechanics, materials science, and general relativity.