filmov
tv
Separable Polynomials and Separable Extensions (Algebra 3: Lecture 14 Video 1)

Показать описание
Lecture 14: We started this lecture by defining what it means for a polynomial f(x) in F[x] to be separable. We then defined what it means for an element that is algebraic over F to be separable and what it means for an algebraic field extension to be separable. We defined the derivative of a polynomial in F[x] and saw that f(x) is separable if and only if it is relatively prime to its derivative. We saw several examples. We then showed that when f(x) is irreducible, it is separable if and only if its derivative is not 0 in F[x]. As a consequence we saw that every irreducible polynomial over a field of characteristic 0 is separable and that every finite extension of a field of characteristic 0 is separable. We saw that an irreducible polynomial over a field of characteristic p is separable if and only if it is not a polynomial in x^p. We defined what it means for a field to be perfect and saw that finite fields are perfect. We proved that if F is a finite field then any irreducible polynomial in F[x] is separable. We concluded the lecture by noting that any finite extension of a perfect field is separable.
Reading: In this lecture we covered most of Section 13.5 of Dummit and Foote. We skipped over the example of Existence and Uniqueness of Finite Fields on pages 549-550. We will come back to this in the next lecture. We also skipped the discussion of separable degree at the end of this section. We may come back to this near the very end of the course.
Reading: In this lecture we covered most of Section 13.5 of Dummit and Foote. We skipped over the example of Existence and Uniqueness of Finite Fields on pages 549-550. We will come back to this in the next lecture. We also skipped the discussion of separable degree at the end of this section. We may come back to this near the very end of the course.
 0:07:59
0:07:59
 0:11:32
0:11:32
 0:13:54
0:13:54
 0:05:57
0:05:57
 0:20:20
0:20:20
 0:27:36
0:27:36
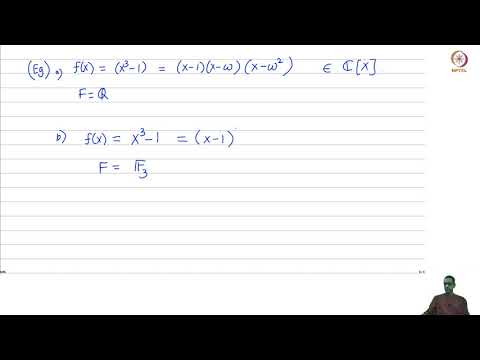 0:22:34
0:22:34
 0:37:31
0:37:31
 0:31:10
0:31:10
 0:09:49
0:09:49
 0:31:37
0:31:37
 0:22:14
0:22:14
 0:16:46
0:16:46
 0:10:24
0:10:24
 0:29:53
0:29:53
 0:46:38
0:46:38
 0:33:54
0:33:54
 0:20:26
0:20:26
 0:30:24
0:30:24
 0:16:13
0:16:13
 0:13:17
0:13:17
 0:17:04
0:17:04
 0:32:23
0:32:23
 0:19:57
0:19:57