filmov
tv
Proof: Cobb-Douglass is Special Case of CES

Показать описание
This video shows that the Cobb-Douglass production function is a special case of the constant elasticity of substitution production function.
Proof: Cobb-Douglass is Special Case of CES
'Cobb-Douglas Utility Function is Special Case of CES Utility Function '
59. IEA: Cobb-Douglas production function as a special case of CES production function
Cobb-Douglas Production Function is the special case of CES production function
Cobb Douglas Production Function
CES is a special case of Cobb Douglas Production Function MEC 101 Microeconomics Analysis IGNOU Eco
Returns to scale Cobb Douglas Production Function
CONVERTING CES FUNCTION INTO COBB-DOUGLAS FUNCTION
The CES Production Function
Slope of CES Isoquants (dK/dL): Possible Cases [Cobb-Douglas, Leontief, Substitutes]
elasticity of substitution of CES production function .
Utility Maximization with a Cobb-Douglas Utility Function
UTILITY FUNCTION ( 4 types)I MICROECONOMICS
Cobb Douglas Production Function
#20 Cobb Douglas Production Function | by Hardev Thakur
53. IEA: Cobb-Douglas production function and its properties
Elasticity of Substitution = 1 for Cobb-Douglas Production Function
finding MPL and MPK from Cobb Douglas Production function
Cobb-Douglas Isoquants
Return to scale for Cobb-Douglas production function
Cobb Douglas Production Function And Elasticity of Substitution | Ecoholics
finding output elasticity of labour and capital from cobb Douglas production function
Cobb-Douglas-Production-Function
Cobb Douglas Function From CES Function (Part-1) Derivation
Комментарии
 0:07:07
0:07:07
 0:19:25
0:19:25
 0:16:12
0:16:12
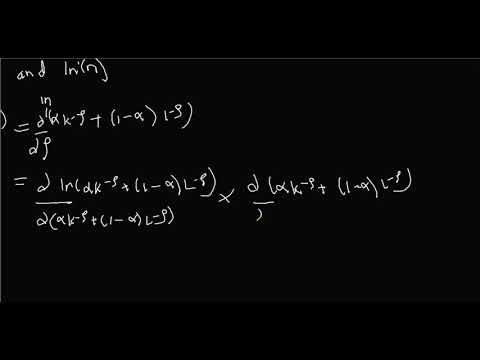 0:20:45
0:20:45
 0:10:50
0:10:50
 0:30:37
0:30:37
 0:06:57
0:06:57
 0:08:00
0:08:00
 0:15:21
0:15:21
 0:12:15
0:12:15
 0:16:20
0:16:20
 0:08:08
0:08:08
 0:06:48
0:06:48
 0:11:50
0:11:50
 0:19:07
0:19:07
 0:32:32
0:32:32
 0:06:37
0:06:37
 0:03:48
0:03:48
 0:08:26
0:08:26
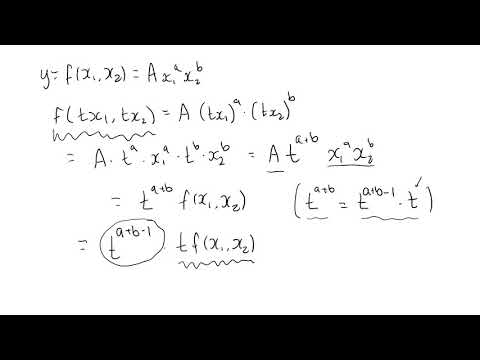 0:04:38
0:04:38
 0:19:13
0:19:13
 0:10:09
0:10:09
 0:02:15
0:02:15
 0:09:25
0:09:25