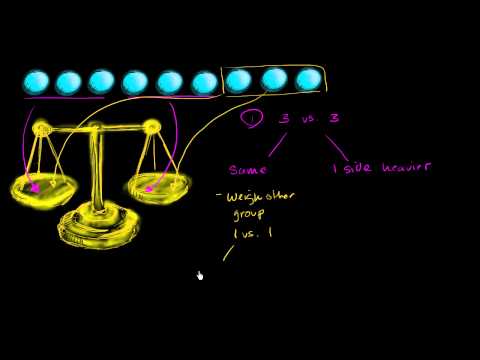
Finding the heavier ball

You have 9 balls that look identical, but 1 is heavier than the rest. What is the minimum number of weighings on a scale to determine the heavy ball?

[WhiteEmerald]

1. Let Khan Academy do the problem. 
2. Therefore....i did it in zero tries. 
3. Earns Nobel Prize in Ballz

[sivapp]

Same puzzle: 9 balls numbered 1-9. One ball differs in weight - heavy or light than others. You have to find the ball & determine whether it is heavy or light. Maximum try allowed is 3. (I solved it.)

[jeffaschwarz]

Disappointed! The still picture for this video gave away the answer.

[BrunoJMR]

i saw this problem, but there were 12 balls, and the different one could be heavier or lighter. it needed 3 uses of the scale though

[zaharakhatoon]

And what will be the pseudocode for above puzzle?

[dineshdeekshith]

There are 10 balls out of which one ball is heavier and all other balls are of equal weight, how many min measurements are required to find the heavier one?

[subductionzone]

I ran into a very similar question long ago where there were twelve balls and you only knew that one ball had a different weight than the others.  You did not know whether it was heavier or lighter.    That problem can be done in three weighings.

[madhavagarwal]

Helped me during a programming contest :)

[sumitmaheshwari]

If we didn't have weighing scale, then let me know how to analyse? .. that was interview question asked in Girnarsoft

[denchi_bryte]

What about 13 balls and you have just 3 attempt to find the heaver ball .

[MrCerialKiller]

8 balls, 2 'weigh ins':
take out two balls, weigh the others with three on each side...
if they weigh is even, you scrap the 6 balls and just weigh the two remaining balls and you're done.
If however the weigh is not even, You scrap the light side and weigh two balls off the heavy side: if even the ball you didn't weigh is the heavy one. If not the heavy ball is the one. 

[masvindu]

2 - the minimum weighs assuming the worst luck.

1 - the minimum assuming the best luck.

[BlueOriginAire]

What if you are given the same instructions and are told that you must use the scales 2 X’s, and no less and no more. Also, you must solve it during class. (Approx 40 min.) On top of that, you will get a 100 as your final grade if correct or a big fat ZERO if you don’t solve it🤪🤯😳.

When you are 16, (and you’re a B student, and you have to pass this class for sufficient credits to graduate next week, )

The added pressure is on to screw with your head

this 9 penny problem will cause a heart pounding indeed.

(I know, it happened to me,
cir. 1982 )

[saff.k]

This fortnite kid said of I answer this correctly he will delete fortnite, thanks Khan academy! (Khan is also my last name lol)

[predo]

With 27 balls, the minimum weighings is 3, right?

[LotsOfBologna]

Alright, I got this. Considering the question is actually "what's the minimum number of weighings to CONSISTENTLY pick out the heavier ball", the answer is 3.
Weigh left 4 vs next 4. If weight the same, ball 9 is heaviest. Else, divide up heavier 4 balls for another weighing.
Divide up heavier 2 balls for another weighing.
You've found your ball.

Now lets watch the video and see if he agrees.

[mikearchives]

It's 1... the *minimum* is 1. If you weigh two balls and one so happens to be the heavy ball, then you know right away.

Other than that, grouping into threes is the best idea. Then the minimum would be 2.

[peter_roth_]

2 weighings in minimum to figure out the heavy one.
Nice brain teaser!
Do you want to think about the same problem with 27 balls? 
Spontaneously I say 6 times to weigh.

[MARSTVCHANNEL]

The possible minimum is 1 weighing, by splitting the balls in 2 groups of 4, and putting them onto the scales, with one ball left unweighted. If the scales are in balance, it means the unweighted ball is the heavier ball, and makes a second weighing unnecessary.

[FizzyToni]

I have a little bit harder problem about weighing these balls. So here it is:


You have 16 balls which weigh 13, 14, 15...28 grams. You need to find the balls which weigh 13, 14, 27 and 28 grams using 26 or less weighings.