Tangent space

Показать описание

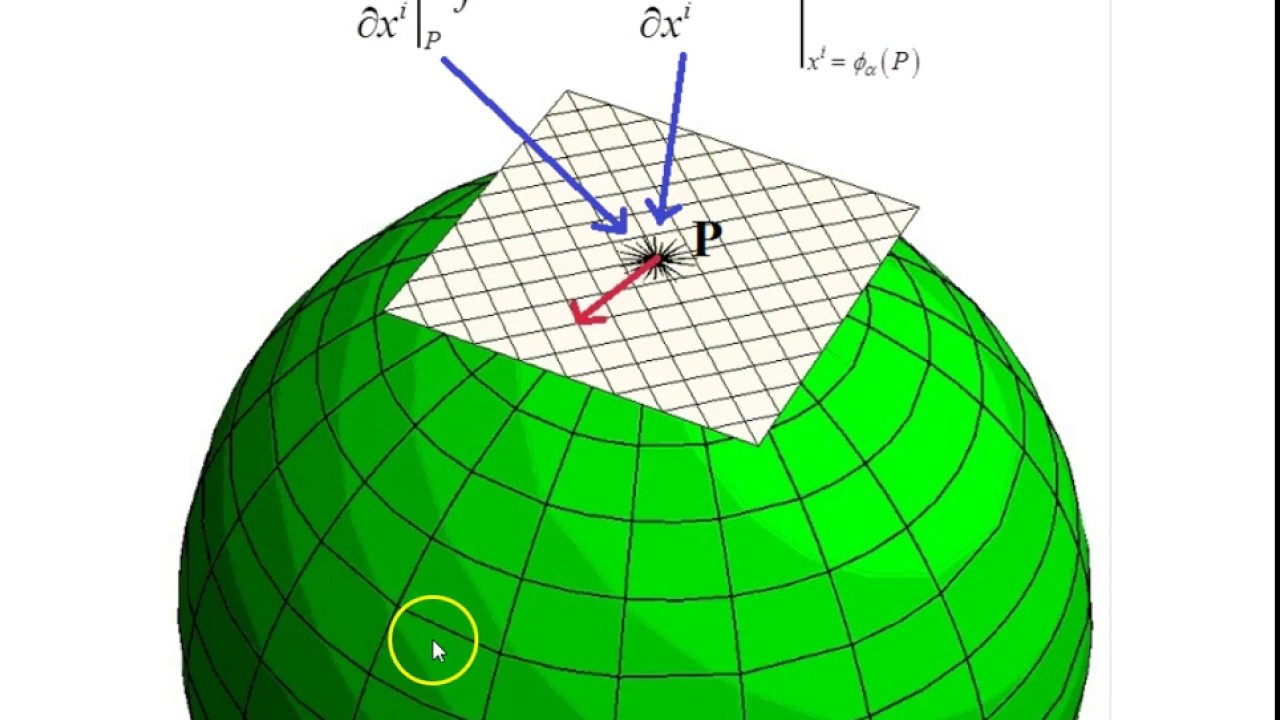
This video looks at the idea of a tangent space at an arbitrary point to any given manifold in which vectors exist. It shows how vectors expressed as directional derivatives form a basis for the tangent space at the given point. This basis has the same dimension as the given manifold.

Рекомендации по теме

Комментарии

I can't imagine how much work you put in to produce these but in my opinion it was definitely worth it

zwitter

Thank-you for your extended Differentiable Manifolds following a question I posed. I have another query in this video and the Hadamard video. In the Hadamard expression using f̂ you have (without the indices): f̂ (x) - f̂(a) = (x - a)f̂(x). But, in accordance with Hadamard's Lemma shouldn't the expression on the right of the equality be ∂f̂/∂x?
Also, you said this is in Euclidean space and if this is the case I understood that all partial derivatives of expressions with different indices are always zero due to orthogonality. So, when you take partial derivatives in index j of terms in x coordinate i, why don't these go to zero?

davidharris

So since we say that f and f^ coincide, meaning the spaces "touch", and the vectors live in the touching space, not the manifold, does that mean that the tangent space *is* the euclidian space the manifold is homeomorphic to at P? I'm not sure if that is a meaningful distinction to draw but it seems to become important when we introduce a metric. Is that metric on the R^n that defines the manifold or is that separate?

narfwhals

24:45 Why didn't you use the product rule to get from the 1sr line to the 2nd?

agnesgosnell

can you kindly provide us with written notes of ur lectures?.these are helpful..

rahmatkhan

What does it mean when you say that the partial derivative of by xi has a direction? If f is scalar valued then so is the partial derivative wrt any single variable, is it not?

misterroboto

Please, make videos on the second and normal fundamental forms to the world sheet of strings in arbitrary background.

tursinbayoteev

This is a perfect example of why the simplification of einstein's equations arrives at a flat universe.

DylanCVlogTV

opus magna...is like a Euler class....

miguelaphan

Tangent space

What are Tangent Spaces in Differential Geometry?

Manifolds #5: Tangent Space (part 1)

Manifolds #5 - Tangent Space (Introduction)

Differential Forms | Introduction and the Tangent Space

Tangent Space

Differential Forms: PART 1A: TANGENT SPACES (INTUITIVELY)

Manifolds 4.1 : Introduction to the Tangent Space

Normal Maps, Tangent Space & IBL • Shaders for Game Devs [Part 3]

Mikołaj Korzyński - Bi-local approach to geometrical optics in GR

12.1 The tangent space - concretely (Commutative Algebra and Algebraic Geometry)

Special Lecture (A Review of Tangent Spaces)

Aspects of the Tangent Space derivation

Game Engine Programming 070.1 - Constructing a tangent space for triangle meshes

Lecture 5: Tangent Spaces (International Winter School on Gravity and Light 2015)

Finding Tangent Space to Cylinder

3D Curves and their Tangents | Intro to Vector-Valued Functions

Analysis II Lecture 12 Part 1 the tangent space

Manifolds #6 - Tangent Space (Detail)

Differential structures: the pivotal concept of tangent vector spaces - Lec 09 - Frederic Schuller

Introduction to submanifolds: definitions and tangent spaces

View, World, Object, & Tangent Space - Shader Graph Basics - Episode 10

21.2 The tangent space to a manifold

Tangent bundle over the sphere

Lec04 - P1 (Basics of Differential Geometry: Tangent Space,Tangent Vectors and Tangent Maps)