Proof: The central angle from two points on a circle is twice the inscribed angle | Class 9 | CBSE

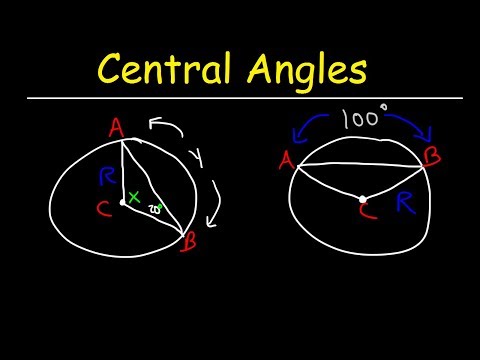
In this lesson, we explore Theorem 9.7 from the NCERT Class 9 Maths book, popularly known as the Central Angle Theorem. This theorem states that the angle subtended by an arc at the center of a circle is double the angle it subtends at any point on the remaining part of the circle. 🎯

I’ll guide you through the theorem step-by-step using two different approaches:
📐 First approach: Using properties of triangles and external angles (NCERT).
📐 Second approach: Using the sum of angles around a point.

👉 If you find this video helpful, don’t forget to like 👍, share, and subscribe to Sunny Sensei for more engaging and educational math lessons!

🎓📘 Additional Geometry Proofs for Practice 🎓📘

🎯 Tangent and Radius Perpendicularity - Circle Theorem: The tangent at any point of a circle is perpendicular to the radius through the point of contact.

🎯 Basic Proportionality Theorem: If a line is drawn parallel to one side of a triangle, intersecting the other two sides at distinct points, it divides those sides in the same ratio.

🎯 AAA Criterion for Similarity of Triangles: If the corresponding angles of two triangles are equal, then their corresponding sides are in the same ratio, and the triangles are similar.

🎯 Central Angle Theorem: The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

🎯 Base Angles Theorem: Angles opposite to equal sides of an isosceles triangle are equal.

🎯 Midpoint Theorem: In a triangle, the line segment joining the midpoints of two sides is parallel to the third side and half as long.

🎯 Pythagoras or Pythagorean Theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

🎯 The Ratio of Areas of Similar Triangles: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.