filmov
tv
Find the last two digits!
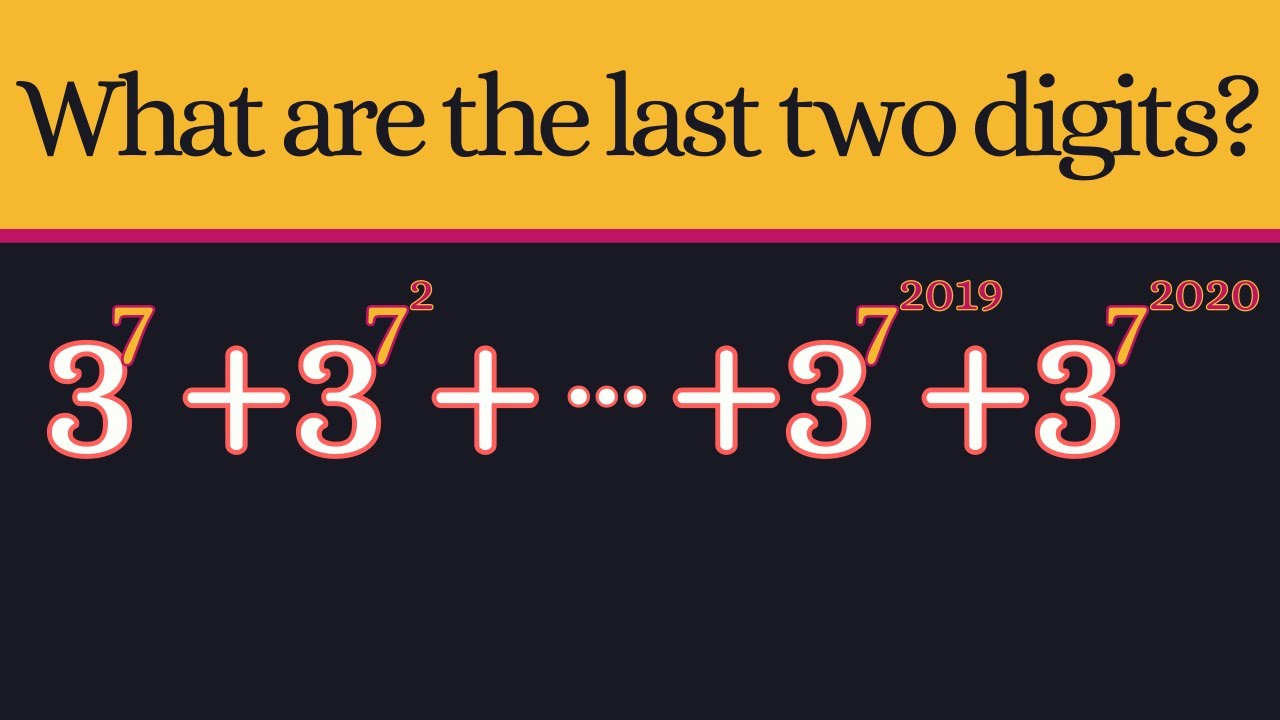
Показать описание
We look at a classic number theory puzzle question.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Calculating Last Two Digits of a Number Raised to Power
Last 2 digits using Euler's Totient Function
Finding the last two digits of a number using modular artihmetic
Find the last two digits.
Find the Last Two Digits of 𝟐^𝟏𝟎𝟎
Last 2 Digits Concept | How to Find the Last Two Digits of a Number | SSC Maths by Mohit Goyal Sir
I7--Last Two Digits
Find the last two digits!
𝐇𝐎𝐖 𝐓𝐎 𝐅𝐈𝐍𝐃 𝐓𝐖𝐎 𝐃𝐈𝐆𝐈𝐓𝐒 𝐒𝐐𝐔𝐀𝐑𝐄 𝐈𝐍 𝐀𝐍𝐘 𝐍𝐔𝐌𝐁𝐄𝐑💯#shorttricks #mathtricks #squaretrick...
Number Theory: How to find the last two digits of powers of a number ending with 3, 7 or 9 - 2^2023
Find Last Two Digits | Olympiad Question
Find the Last Two Digits | Numbers | CAT/MAT/Management Exams
Last 2 Digits Concept - How to Find the LAST TWO DIGITS of a Number - Master Class by MJ
How to Find Last Digits of Large Powers and Exponents | GMAT Shots | Experts' Global GMAT Prep
How to find the last two digits of a number ending in 5 | [ Number Theory ]
Challenge 68: Can You Find the Last Two Digits?
Last Two Digits of This Number? No Calculators!!
Find the last two digits of a number ending in 1 | [ Number Theory ] | For all Exams
Finding Last Two Digits Trick
How to Find The Last 2 Digits of A Large Number Written in Exponent Form
521 math #127: The last two digits (Euler's Totient Function?)
find the Last Two Digits I Number System I GATE ESE SSC HAL & Others I By Saurabh Sir
How to Find the last two digits of Long Multiplication
Last Two Digit short tricks | How to Find out last two Digits #ssccgl #sscgd #ssc #sscchsl
Комментарии
 0:14:02
0:14:02
 0:17:15
0:17:15
 0:10:30
0:10:30
 0:12:28
0:12:28
 0:07:32
0:07:32
 0:30:33
0:30:33
 0:01:15
0:01:15
 0:16:14
0:16:14
 0:00:45
0:00:45
 0:13:34
0:13:34
 0:03:17
0:03:17
 0:13:15
0:13:15
 0:46:35
0:46:35
 0:01:59
0:01:59
 0:04:08
0:04:08
 0:01:19
0:01:19
 0:10:01
0:10:01
 0:04:07
0:04:07
 0:05:21
0:05:21
 0:47:51
0:47:51
 0:08:01
0:08:01
 0:38:05
0:38:05
 0:08:10
0:08:10
 0:00:54
0:00:54