Optimization: Find Dimensions of Rectangle With Largest Area Inscribed in a Circle

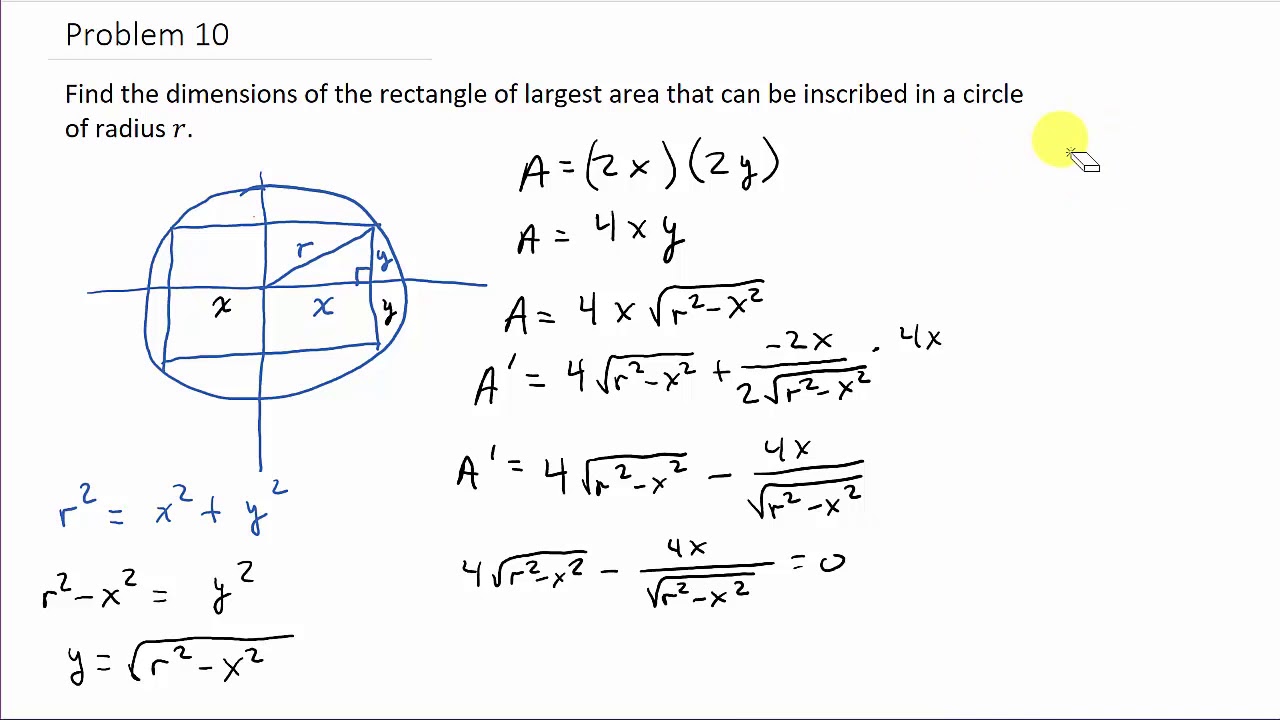
This video shows how to find the dimensions of a rectangle with largest area that can be inscribed in a circle of radius r.

[cesium]

your accent helps me pay attention i have no idea why

[幻彩小羽毛]

I have a homework question with the exact same same question lol, this was really helpful

[ethandoest]

This video is going to save my final grade!! This solution makes sense now!!

[kainime]

Sir I am new to your channel and your explanation amazing it is clear as a crystal of water

[rezanhammo]

Midterm exam tomorrow, I really appreciate this video

[oliviawoloshyn]

Love your voice and this explanation is really easy to follow
big thumbs up

[RahooMohammadi-czes]

Can you please help me

So i was thinking what if the tye rectangle has a length of 11 cm and width of 6 cm.
How do we solve that ??

[jfig]

so are we solving for 2x at the end rather than singular x or y?? i was bit confused.

[Waltu]

Shouldn't the second term for the derivative of the area be -4x^2/sqrt(r^2-x^2) instead of -4x/sqrt(r^2-x^2)? -x*4x= -4x^2.

[maheralabbar]

I have a question. Why can’t the area just be xy. Like would it still work. I tried it with radius 4 and I am getting 8 as my area.
I don’t get why it has to be (2x) (2y) is there something else to do instead of splitting it into fourths

[adamvaught]

How did the r disappear at the end? Shouldn’t it be r-r/2^1/2?

[faithfury]

Hi! i have a question, why r^2 is a constant for this example? i saw time rates with the radius getting derived at, isn't it the same with optimization?

[eduardobarragan]

How would you find the radius of the entire circle?

[basrocker]

Thankyou sir!. This was pretty helpful.

[Maya-xsxn]

Thank you, it really help me understand the problem.

[Somm_RJ]

Why would you need to do all that?

A square is a rectangle.

You just have to draw a line (radius) from the center, let's call this A. Then, another line (radius) at 90° of the first line, Let's call this B. Now, you already have 2 sides of a triangle, just calculate the hypothenus using Pythagorean Theorem using the 2 sides above, sqrt(A^2+B^2). Because the 2 sides (A and B) are equal, same as the length of the radius (r), you can simplify this by doing sqrt(2r^2).

Or you can alternatively, you can use the sine function, r/sin 45°, since the resulting triangle would be an isosceles triangle and you have a given 90° on 1 angle.

The result would be 1 side of the rectangle. Since it is a square, then you just multiply it by itself.

In simplest form, it would look like this,

Area=sqrt(2r^2)^2

Alternatively,

Area=(r/sin 45°)^2

[qalbabbas]

You should find second derivative and find Local maximum and minimum for area, which can give surety for maximum area

[kainime]

Sir I am new to your channel and your explanation amazing it is clear as a crystal of water