filmov
tv
Oxford University Admissions Question - Can You Solve It?

Показать описание
University of Oxford Mathematician Dr Tom Crawford presents a question used in the 2021 Maths Admissions Interviews.
For more maths content check out Tom's website
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
For more maths content check out Tom's website
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
Oxford University Maths Admissions Test 2023 Question 10
Can you solve this Oxford admissions question?
Oxford University Admissions Question - Can You Solve It?
Oxford Admissions Question (No Calculator)
Oxford University Admissions Interview Question with Solution
Oxford University Maths Admissions Test 2023 Question 9
Oxford University Maths Admissions Test 2023 Question 2
Oxford University Maths Admissions Test 2023 Question 8
2016—2018 past papers | MAT livestream 2024
How Hard is it to Get Into Oxford University?
Oxford University Maths Admissions Test 2023 Question 1
Oxford University Maths Admissions Test 2023 Question 4
Oxford University Maths Admissions Test 2023 Question 7
Oxford University Maths Admissions Test 2023 Question 3
Oxford Maths Admissions Interview Question with @blackpenredpen
Oxford University Maths Admissions Test 2023 Question 6
Oxford University Maths Admissions Test 2023 Question 5
A very tricky Oxford University Admission Algebra Exam | Entrance Aptitude Test | Find x!!
Oxford Admissions Question: Done in Seconds if You Know the Trick
Why Did You Choose This University? BEST ANSWER to this University Admissions Interview Question!
Oxford University Mathematician takes Cambridge Entrance Exam (STEP Paper) PART 1
Sample #Oxford Uni MATHEMATICS interview!
Admissions interview - typical maths question.
Oxford University Admissions Interview Question: What is the optimal size for a tin of cat food?
Комментарии
 0:01:00
0:01:00
 0:08:18
0:08:18
 0:00:49
0:00:49
 0:03:19
0:03:19
 0:04:59
0:04:59
 0:00:59
0:00:59
 0:01:00
0:01:00
 0:00:51
0:00:51
 2:03:42
2:03:42
 0:13:22
0:13:22
 0:01:00
0:01:00
 0:00:58
0:00:58
 0:00:58
0:00:58
 0:01:00
0:01:00
 0:18:44
0:18:44
 0:01:00
0:01:00
 0:00:57
0:00:57
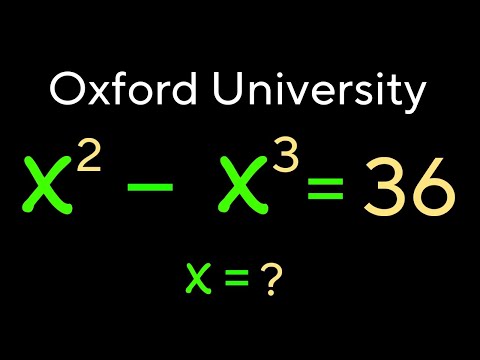 0:09:23
0:09:23
 0:03:22
0:03:22
 0:05:53
0:05:53
 1:36:55
1:36:55
 0:15:20
0:15:20
 0:03:24
0:03:24
 0:11:20
0:11:20