filmov
tv
Laplace Transform With Unit Step Functions :: Second Shifting/Translation Theorem

Показать описание
In this video we discuss how to take Laplace Transforms of functions involving the unit step function.
The unit step function is a function that has a value of zero then takes a value of 1 (turns on) at some value 'a' and stays on forever after.
Graphical examples of functions involving unit steps are presented.
The second translation theorem tells us how to take the Laplace Transform of such functions.
The second shifting theorem in its first form is
L{f(t-a) U(t-a)} = F(s) e^(-as)
This form is more useful when taking inverse Laplace Transforms.
The second shifting theorem alternate form is
L{g(t)U(t-a)} = e^(-as) L{g(t+a)}
This form is more commonly encountered when computing the Laplace Transform.
-------------------------
I'm Jonathan, I'm excited to share with you what little I know about Laplace Transforms and unit step functions and how they're used.
Thanks for watching!
The unit step function is a function that has a value of zero then takes a value of 1 (turns on) at some value 'a' and stays on forever after.
Graphical examples of functions involving unit steps are presented.
The second translation theorem tells us how to take the Laplace Transform of such functions.
The second shifting theorem in its first form is
L{f(t-a) U(t-a)} = F(s) e^(-as)
This form is more useful when taking inverse Laplace Transforms.
The second shifting theorem alternate form is
L{g(t)U(t-a)} = e^(-as) L{g(t+a)}
This form is more commonly encountered when computing the Laplace Transform.
-------------------------
I'm Jonathan, I'm excited to share with you what little I know about Laplace Transforms and unit step functions and how they're used.
Thanks for watching!
Laplace Transform of a Piecewise Function (Unit Step Function)
Laplace transform of the unit step function | Laplace transform | Khan Academy
Laplace Transform of Basic Signals (Unit Step Signal)
Solve differential equation with Laplace Transform involving unit step function
Laplace Transform of Unit Step Function | AEM Video 1
Laplace Transform of Unit Step Function u(t-a)
Laplace transform of unit step function, sect7 6#1
Laplace Transforms with Unit Step Functions
Laplace Transform and ROC of Standard Signals | Laplace Transform of Impulse Function, Signal System
Laplace Transform and Piecewise or Discontinuous Functions
Laplace transform of unit step function second problem(PART-2) by easy maths easy tricks
Differential Equations | Laplace Transform of a Piecewise Function
Unit Step Function- Laplace Transform|GYMAT101 Group B&C|S1 module3 |MAT102 S2 Module 4| Part14
Laplace transform of unit step function & rectangular window function
Inverse Laplace Transform with unit step function, sect7.6#15
Laplace Transform 10 – Unit Step Functions | Heaviside Functions | Piecewise Functions with Examples...
Ex: Find the Laplace Transform of a Step Function (method #1)
Laplace transform of unit step function fourth problem(PART-4) by easy maths easy tricks
Inverse Laplace transform with unit step function, sect7.6#13
Unit Step Function | Heaviside Function | Problems | Laplace Transform | Maths
Laplace transform of f(t-a)u(t-a), the shifted unit step function
Unit Step Function Laplace Transform | Laplace Transform of Heaviside Unit Step Function | Example
Unit Step Function Laplace Transform Vtu 7 Marks Important Question💯🔥
Unit Step Function | Laplace transform | part 21 l #BarunMaths
Комментарии
 0:06:27
0:06:27
 0:24:15
0:24:15
 0:05:01
0:05:01
 0:07:06
0:07:06
 0:21:06
0:21:06
 0:04:28
0:04:28
 0:02:16
0:02:16
 0:12:24
0:12:24
 0:22:27
0:22:27
 0:12:00
0:12:00
 0:07:14
0:07:14
 0:04:44
0:04:44
 0:22:52
0:22:52
 0:07:07
0:07:07
 0:07:27
0:07:27
 0:27:54
0:27:54
 0:05:50
0:05:50
 0:07:09
0:07:09
 0:03:52
0:03:52
 0:16:15
0:16:15
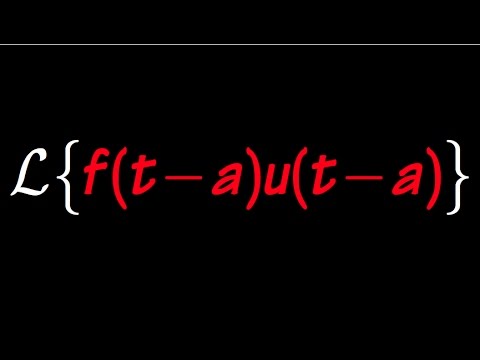 0:12:16
0:12:16
 0:30:33
0:30:33
 0:10:32
0:10:32
 0:16:33
0:16:33