Cycloid — The Brachistochrone Curve

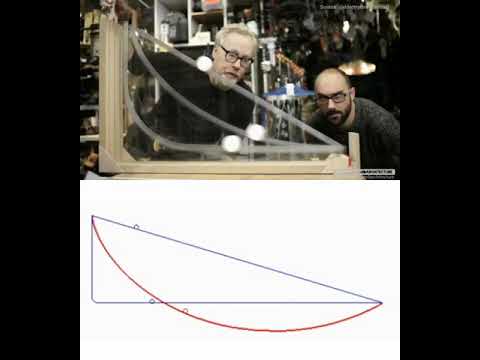
The cycloid is a curve created by a point on the rim of a rolling circle defined by its parametric equations. It features periodicity, sharp cusps, and the property of being a tautochrone curve. Most notably, the cycloid is the solution to the brachistochrone problem, determining the path of quickest descent under gravity between two points. This discovery was crucial in the development of the calculus of variations. The cycloid exemplifies the practical application of abstract mathematical principles in solving real-world problems.

This video is produced with the animation engine Manim.

Mscene — Science Animation

Thanks for watching!
CuriousWalk

[AKfire]

Very good visuals and explanation.. good work

[JohnHainesProjekts]

This video is excellent! I'm in the process of constructing a skate ramp (mini ramp) using a brachistochronic curve to see whether its properties make it superior to other transition types but is there an easier way to draw the curve than cutting out a large disc, embedding a marker into the surface and rolling? Thanks!

[stevenpalmore]

Perfect ...could use old cd disc for the drawing aide

[AKfire]

Could you please share the full code for the whole of the video.. The one that you've shared is only for the creation of cycloid, not for the whole video..

[AKfire]

Please share the code for the full video.

[rk]

That was awesome. Thank you. My question is: at what point up the curve will a straight line be faster?

[MathPhysicsEngineering]

I also made a video about modeling the cycloid
check a video on my channel called:
Modeling The Cycloid in Desmos, The Brachistochrone problem and Spiderman