filmov
tv
Analytic Geometry - The orthonormal system

Показать описание
A coordinate system is a two-dimensional number line, for example, two perpendicular number lines or axes.
The horizontal axis is called the x-axis and the vertical axis is called the y-axis
The center of the coordinate system (where the lines intersect) is called the origin. The axes intersect when both x and y are zero. The coordinates of the origin are (0, 0).
An ordered pair contains the coordinates of one point in the coordinate system. A point is named by its ordered pair of the form of (x, y). The first number corresponds to the x-coordinate and the second to the y-coordinate.
To graph a point, you draw a dot at the coordinates that corresponds to the ordered pair. It's always a good idea to start at the origin. The x-coordinate tells you how many steps you have to take to the right (positive) or left (negative) on the x-axis. And the y-coordinate tells you have many steps to move up (positive) or down (negative) on the y-axis.
The horizontal axis is called the x-axis and the vertical axis is called the y-axis
The center of the coordinate system (where the lines intersect) is called the origin. The axes intersect when both x and y are zero. The coordinates of the origin are (0, 0).
An ordered pair contains the coordinates of one point in the coordinate system. A point is named by its ordered pair of the form of (x, y). The first number corresponds to the x-coordinate and the second to the y-coordinate.
To graph a point, you draw a dot at the coordinates that corresponds to the ordered pair. It's always a good idea to start at the origin. The x-coordinate tells you how many steps you have to take to the right (positive) or left (negative) on the x-axis. And the y-coordinate tells you have many steps to move up (positive) or down (negative) on the y-axis.
Analytic Geometry - The orthonormal system
Orthogonality and Orthonormality
Analytic Geometry
Introduction to orthonormal bases | Linear Algebra | Khan Academy
Analytic Geometry
BMA1205: ANALYTICAL GEOMETRY LESSON 1
scalar product of collinear orthogonal vectors
Analytic Geometry - Inner product / Orthonormal basis/orthogonal matrix/Orthogonal Projection
Analytic Geometry P 4
Analytic Geometry Equations of a Line Part 1 of 3
Analytic Geometry: The Circle
orthonormal system
Vector and Analytic Geometry - Parallel and Orthogonal Vectors
Analytical Geometry Grade 12 Exam Question
Analytical Geometry and Linear Algebra (CS) Lecture, 2 Oct 2020
Analytic Geometry Part 1 - Lines
Analytic Geometry - Solutions of Graphs
Analytical solid geometry : - ( Orthogonal spheres ; Solving problem ) - 83.
2.1 Analytic Geometry I
Analytic geometry of planes | Lecture 6 | Vector Calculus for Engineers
Analytical Geometry and Linear Algebra (CS) Lecture, 25 Sep 2020
Plotting Points In a Three Dimensional Coordinate System
Analytic Geometry: Rectangular, Cylindrical and Spherical Coordinate System
Analytic Geometry Preliminary Concepts
Комментарии
 0:04:28
0:04:28
 0:11:48
0:11:48
 0:04:37
0:04:37
 0:11:16
0:11:16
 0:00:16
0:00:16
 1:43:33
1:43:33
 0:15:08
0:15:08
 0:17:53
0:17:53
 0:11:22
0:11:22
 0:57:00
0:57:00
 0:27:08
0:27:08
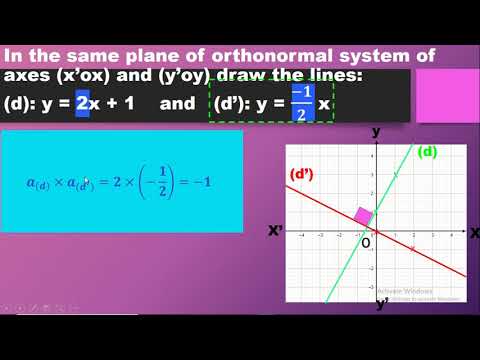 0:19:07
0:19:07
 0:05:28
0:05:28
 0:15:57
0:15:57
 1:44:15
1:44:15
 1:32:11
1:32:11
 0:08:01
0:08:01
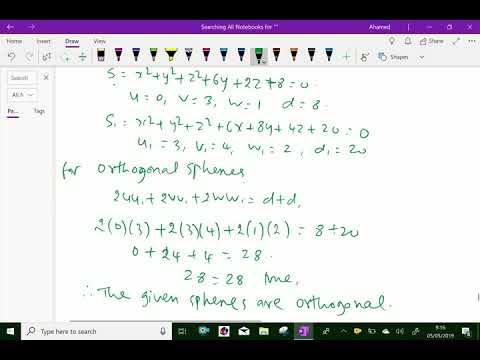 0:05:30
0:05:30
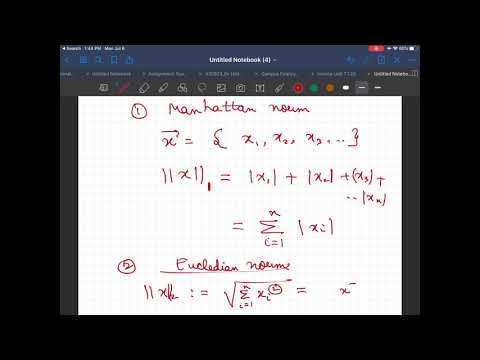 0:25:02
0:25:02
 0:12:59
0:12:59
 1:38:08
1:38:08
 0:07:27
0:07:27
 0:06:56
0:06:56
 0:28:57
0:28:57