filmov
tv
An integral starring Gauss!

Показать описание
This integral has a bunch of x and ln(x) in it...but Gauss is hiding in there after a little substitution!
New math videos every Monday and Friday. Subscribe to make sure you see them!
An integral starring Gauss!
An Epic Way To Do The Gaussian Integral
Integration by Parts and using the Gaussian Integral!
Gaussian Integral
2017 MIT Integration Bee - A Hidden Gaussian Integral!
Integrate with Feynman's trick and Gaussian Integral
A most general solution to the Gaussian Integral
A Spicy Gaussian Integral? - MIT Integration Bee Question
Gaussian Integral
The Gaussian Integral
Children of the Gaussian Integral
2017 MIT Integration Bee (8) - A Gaussian Integral!
Gaussian Integral with a (Reciprocal) Twist: Berkeley Integration Bee (1)
A Gaussian-like integral evaluated using partial differentiation: ∫exp(−ax²−b/x²)dx
Gauss coming in clutch - MIT integration bee (2020 qualifiers, Q20)
Improper integral including ln natural log and gaussian e^(-x^2)
Intégrale de Gauss - Calcul détaillé
Gaussian integral using change of variables
A basic integral - know your strategies!
Gaussian Integration (Part 3)
Exo : Intégrale de Gauss par les intégrales de Wallis : changements de variable à répétition
Another monster integral
Integral with some Very Big Powers
MIT INTEGRATION BEE 1
Комментарии
 0:07:09
0:07:09
 0:03:41
0:03:41
 0:05:32
0:05:32
 0:00:52
0:00:52
 0:06:04
0:06:04
 0:01:02
0:01:02
 0:07:42
0:07:42
 0:06:42
0:06:42
 0:06:39
0:06:39
 0:09:49
0:09:49
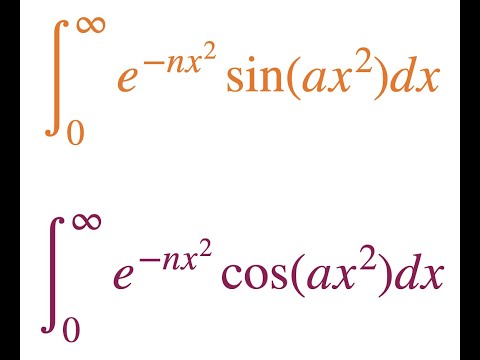 0:19:21
0:19:21
 0:01:45
0:01:45
 0:10:22
0:10:22
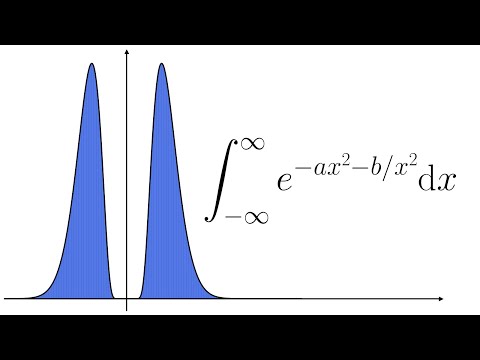 0:12:27
0:12:27
 0:07:26
0:07:26
 0:02:01
0:02:01
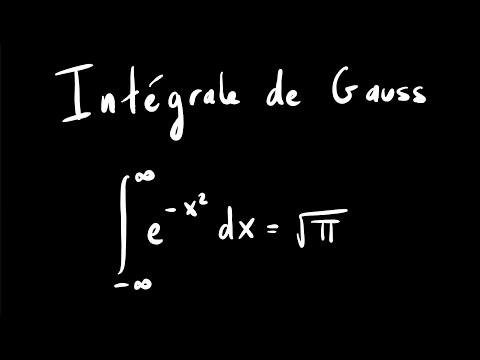 0:13:41
0:13:41
 0:08:07
0:08:07
 0:03:36
0:03:36
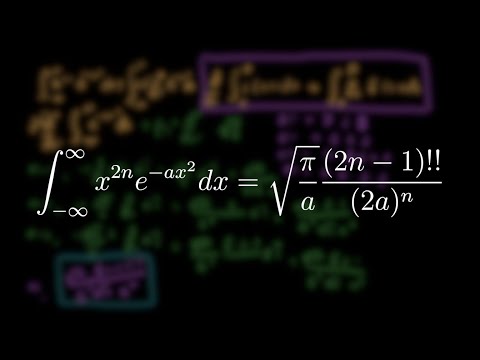 0:11:15
0:11:15
 0:05:29
0:05:29
 0:20:26
0:20:26
 0:04:35
0:04:35
 0:07:33
0:07:33