Understanding Mergesort: Sorting Made Simple | Recursion Series

Mergesort is a well-known and efficient sorting algorithm that follows the divide-and-conquer paradigm. It aims to sort a given array or list of elements by dividing it into smaller subarrays, sorting those subarrays recursively, and then merging them back together to obtain the final sorted result.

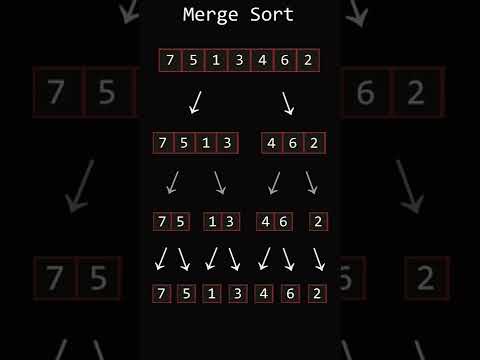
The algorithm begins by repeatedly dividing the input array into two halves until each subarray contains only one element or is empty. This process is known as the "divide" step. Then, it merges adjacent pairs of these subarrays, comparing and rearranging the elements in a sorted order. This merging process continues until a single sorted array is obtained, hence the term "merge" in mergesort.

One of the key advantages of mergesort is its stability, meaning that elements with equal values retain their original relative order after sorting. This property makes mergesort particularly useful in scenarios where preserving the original order of equal elements is crucial.

Mergesort exhibits a time complexity of O(n log n), where "n" represents the number of elements in the input array. This efficiency makes mergesort suitable for sorting large datasets, and it is often used as a standard benchmark for other sorting algorithms.

Overall, mergesort's simplicity, stability, and efficient performance have made it a popular choice in various applications, ranging from general-purpose sorting to applications in data analysis, parallel computing, and more.

0:00 Mergesort overview
2:15 Algorithm animation
3:35 The divide phase
5:10 The conquer phase
5:53 Mergesort pseudocode
7:46 Merge function

Source code repository:

Video slides:

[OleksandrTodosiienko-iu]

Cool, with animated explanation it`s so much easier to understand!

[rosyidharyadi]

I'm currently self-learning computer science and my main book is Skiena's. While the book is amazing, sometimes it's just hard to grasp. This channel is really good as a supplementary

[zxzDanielDefo]

Hi, appreciate your work!
Here's the list of topics I'd love you to make videos on:
1. Complexity theory: P, NP, etc problems, categorization and how they relate to coding interviews
2. Cover problem solving techniques: sliding window, two pointers, backtracking, etc
3. Cover all sorting methods and their applications
4. Bit manipulations, performance gains, how to optimize a solution to use bits

❤

[levon]

Really nicely done, very clear. Thank you for sharing.

[fromjavatohaskell]

4:24 please consider updating formula for mid point calculation mid = (lo + hi) /2 that might overflow with mid = lo + (hi - lo) / 2

[shnerdz]

Love your videos! Please consider making some on segment trees. I feel like there aren't great ones out there right now

[kaushikkundu]

First time watching video of yours. Great video

[WillLanham-sn]

great explanation and pseudocode example! Thankyou!

[JAMESMAYENMANYUAT]

It is interesting and understandable ❤❤❤

[talhataki]

I was wondering which software you use for creating such vibrant illustrations? Is it free to use or open-sourced?

[vidorg]

Do you have videos about amotized analysis?

[joelsanfeliu]

I comment here because it's your last video and i don't know how to reach to you. If you or actually anyone can help me with this i'll be very greatful. Given a input of a lot of words and an NxM dimension i have to create an algorithm that designs the best (if possible, or one of the bests) sigle-finger NxM keyboard layout for mobile. Which means that, for example, given a letter in the keyboard it's better to have closer letters that you know that with highly probability will come next. An other statement could be that the middle part of the keyboard is best to reach from the finger so it should be the most freqüent letter, so the most important letters should councentrate in the middle meanwhile you consider what i said before about you have closer letters that you know that with highly probability will come next and also you consider the NxM keyboard layout. The frequency of each letter and what letters come next after a certain letter it's easy to get by reading the input words and storing it in a data structure, but once i have this i don't know how to do this algorithm. Obviously you have to find the best combination of letters in the keyboard layout so this if you do it by bruteforce it's exponential and it's impossible to do it in an efficient way. But even if i could, i don't even know how to judge each combination and know which one is the best. I though about making it a graph and get something or even the google's pagerank algorithm which has a similarity, but i got stuck. I also thought about genetic algorithms which would be so efficient to find the best or one of the best, which that's enough. I don't know if i explained myself clearly, if not i'll try to explain it in different words or something. Thanks.

[kvelez]

def merge(left, right):
sorted_list = []
l, r = 0, 0
while l != len(left) or r != len(right):
if l == len(left):
sorted_list.append(right[r])
r += 1
elif r == len(right):
sorted_list.append(left[l])
l += 1
elif left[l] < right[r]:
sorted_list.append(left[l])
l += 1
else:
sorted_list.append(right[r])
r += 1
return sorted_list
print(merge([1, 3, 5, 7], [2, 4, 6, 8]))

[alifrahman]

when the world needed him most... he vanished 😔