Precalculus - 15

A college course for functions:
Module 1: Basic Concepts of Functions and Inverse functions
review of function notation
definition of a function; i.e. functions as machines with input and output
the sets domain and range
the vertical line test
piece-wise functions, mostly give examples where all pieces are linear
average rate of change (independent of lines), examples with linear, quadratic, exponential, and power functions
composition of functions
one-to-one functions, what it means and the horizontal line test
inverse functions – definition
finding inverse functions
graphing inverse functions

Module 2: Polynomial functions
Definition of polynomials, degree, leading term, constant term, mention quadratic functions and power functions with positive exponents as an example
long-run behavior of polynomials
review finding the vertex of quadratic functions and graphing
zeros of polynomials - need to know what zeros of a polynomial are, understand the relationship between factored form of a polynomial and the graph, should also know that there can be at most as many x-intercepts as the degree of the polynomial
review finding the x-intercepts of quadratic functions via (1) graphing, (2) factoring, (3) taking the square root, and (4) the quadratic formula

Module 3: Rational Functions
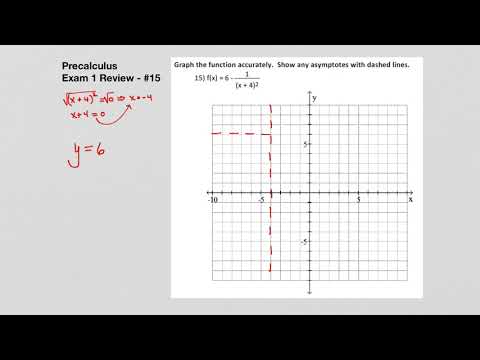
identify where the graph of a rational function will have holes and vertical/horizontal asymptotes; students should have an understanding of why the graph has these features that goes beyond just going through steps in a procedure
students should be able to graph rational functions in a graphing software and make sense of the resulting graphs

Module 4: Exponential and Logarithmic Functions
solving exponential equations
review the formula for exponential functions, graphing, and horizontal asymptotes
introduce the natural number e through the example of compound interest
the formula for exponential functions
finding the formula for an exponential function given the y-intercept and one other point
finding the formula for an exponential function given any two points
Logarithms Functions as the inverses of exponential functions
graphs of logarithms, vertical asymptotes
evaluating logarithmic expressions
properties of logarithms

Module 5: Trigonometry with circles & triangles
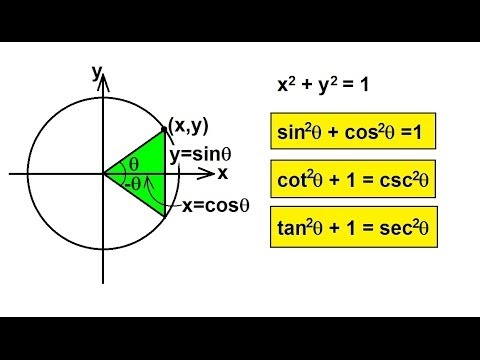
the initial and terminal arms of angles, angles in the unit circle, coterminal angles
radians in the unit circle
converting between degrees and radians
definition of sine, cosine, tangent, cosecant, secant, and cotangent for right triangles
using 45-45-90 and 30-60-90 triangles to find the sine, cosine, tangent, cosecant, etc. of angle written in radians in the circle
solving trigonometric equations
graphs of Trigonometric Functions
graphs of trigonometric functions, do all of them but special emphasis and much more time spent on sine, cosine, and tangent

Module 6: Transformations of Functions
shifts, stretches, and reflections
start by doing examples with trigonometric functions but then do examples with other functions as well such as polynomial, rational, exponential, and logarithmic functions
analytic Trigonometry
simplifying expressions using the basic trigonometric identities: reciprocal identities, , Pythagorean identity, even/oddness of sine/cosine.