Coefficient of Rank Correlation: Part 1 Introduction and Basics

Rank Correlation is a statistical technique used to measure the degree of association between two ranked variables. It assesses how well the relationship between two variables can be described using a monotonic function. Rank correlation is often used when data does not meet the assumptions of parametric tests, or when the data is ordinal.

Two widely used methods for calculating rank correlation are Spearman’s Rank Correlation Coefficient and Kendall’s Tau.

1. Spearman’s Rank Correlation Coefficient (ρ or r_s)
Spearman’s rank correlation is a non-parametric measure that assesses the strength and direction of the association between two variables based on the ranks of the data points.

Formula:
𝑟
𝑠
=
1
−
6
∑
𝑑
𝑖
2
𝑛
(
𝑛
2
−
1
)
r
s
​
=1−
n(n
2
−1)
6∑d
i
2
​

​

Where:

𝑑
𝑖
d
i
​
= difference between the ranks of corresponding variables
𝑛
n = number of observations
Steps to calculate Spearman’s Rank Correlation:
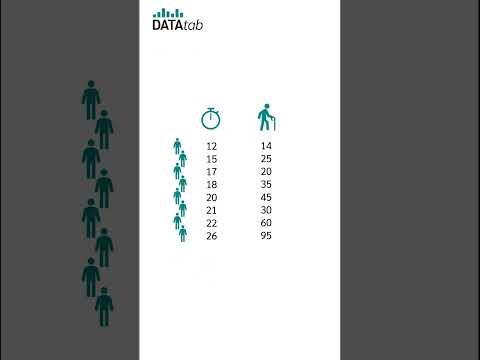
Rank the data for both variables (assign ranks starting from 1).
Calculate the differences between the ranks for each pair of observations.
Square these differences.
Substitute the values into the formula.
2. Kendall’s Tau (τ)
Kendall’s Tau is another non-parametric statistic that measures the strength of dependence between two variables. It is based on the number of concordant and discordant pairs of observations.

Formula:
𝜏
=
(
𝐶
−
𝐷
)
1
2
𝑛
(
𝑛
−
1
)
τ=
2
1
​
n(n−1)
(C−D)
​

Where:

𝐶
C = number of concordant pairs
𝐷
D = number of discordant pairs
𝑛
n = number of observations
Uses of Rank Correlation
Ideal for data that is ordinal or not normally distributed.
Can handle ties (when two or more values are equal) with appropriate adjustments.
In Part 2, we can delve deeper into the interpretation of Spearman's and Kendall's results and examples for real-world applications.
\

#Statistics #DataAnalysis #StatisticalLearning #MathTutoring #LearningStatistics #DataScience #StudyMath #StatisticalTechniques
Rank Correlation Specific #RankCorrelation #SpearmansRank
#SpearmanCorrelation #KendallsTau #CorrelationCoefficient
#CorrelationAnalysis #NonParametricStatistics
#MathEducation #OnlineLearning #StudyTips #LearnWithMe #StudentLife
#MathTeachers #StudyMotivation #MathHelp #StatisticsForBeginners
#MathChallenge #LearnEveryday #DataDriven

@perfectcommerceconcepts

correlation and regression,correlation,correlation coefficient,rank correlation,positive correlation,what is correlation,linear correlation,introduction of rank correlation,introduction to correlation,spearman's rank correlation,spearman's rank correlation coefficient,rank correlation coefficient,correlation and regression in statistics,rank correlation definition and formula,correlation and regression analysis,coefficient of correlation,negative correlation