filmov
tv
2.16 Limits and composition of functions
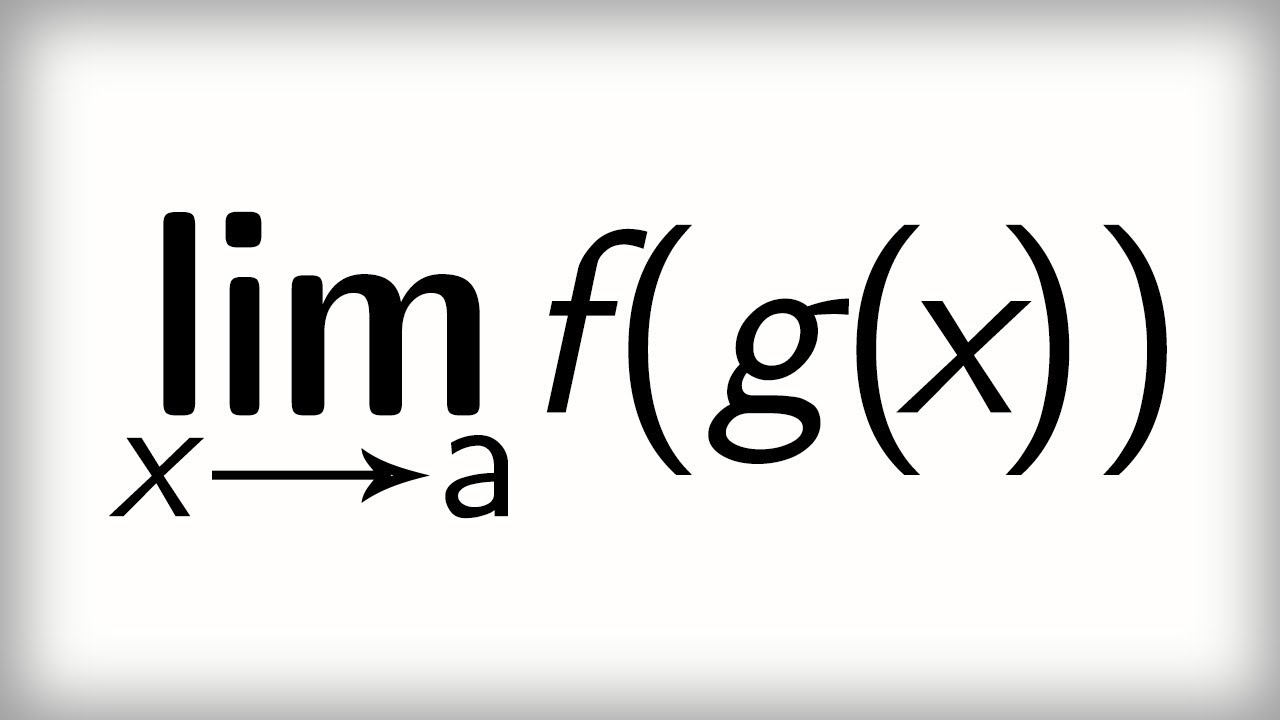
Показать описание
There isn't a nice law for limits of compositions of functions: knowing that two functions have limits does not tell me whether the composition has a limit. Why? And what can we do instead?
Related videos:
0:00 Introduction
1:10 False composition theorem
1:46 Composition continuity
2:02 Counter-example
3:42 Core of the problem
5:59 Fixing the theorem
7:23 Final notes
Composite Functions
Piecewise Functions - Limits and Continuity | Calculus
Limits - Algebraic Properties, Substitution Theorem, and Composition of Functions
2 2 Definition of derivative using limits composition rationalize numerator
Composition of Functions and Domain 🔥Calculus | Math with Mr Barnes
9 Trig Limits and Composition of Limits
Camera Basics - Aperture
Squeeze theorem or sandwich theorem | Limits | Differential Calculus | Khan Academy
Function composition limit - GRE Mathematics Subject Test
continuity of composition functions
Finding the Composition of Two or More Functions | T9 #2 #shorts #functions #composition #mathisfun
Intermediate Value Theorem
Continuity Basic Introduction, Point, Infinite, & Jump Discontinuity, Removable & Nonremovab...
U-substitution With Definite Integrals
How to Answer Any Question on a Test
Recursive Formulas For Sequences
Do You Have 'Good' or 'Bad' Muscle-Building Genetics? (5 SIGNS)
Evaluating composite functions example | Functions and their graphs | Algebra II | Khan Academy
Calculus 1 Final Exam Review
Class 12th – Composition of Functions | Continuity and Differentiability | Tutorials Point
Composition of Functions
[GCC Math 101/120 Common Final Sample 1] (Q16.) Function Composition
Topic 1.5 Review Composition limits with graphs
Composition of Functions
Комментарии
 0:05:23
0:05:23
 0:10:06
0:10:06
 0:23:21
0:23:21
 0:19:49
0:19:49
 0:20:25
0:20:25
 0:21:16
0:21:16
 0:05:19
0:05:19
 0:07:11
0:07:11
 0:05:38
0:05:38
 0:08:47
0:08:47
 0:00:39
0:00:39
 0:11:04
0:11:04
 0:13:31
0:13:31
 0:11:03
0:11:03
 0:00:27
0:00:27
 0:02:54
0:02:54
 0:08:50
0:08:50
 0:04:11
0:04:11
 0:55:58
0:55:58
 0:04:14
0:04:14
 1:23:59
1:23:59
 0:04:35
0:04:35
 0:17:41
0:17:41
 0:22:04
0:22:04