filmov
tv
Class: 9th | Mathematics (FBISE) | Lecture # | Unit #12 | Theorem #12.1.1 |
Показать описание
Class: 9th |
Mathematics (FBISE) |
Lecture # |
Unit #12 |
Theorem #12.1.1 |
Mathematics Science group |
Any point on the right bisector of a line segment is equidistant from its end points |
Dear viewers, it is my pleasure to deliver you mathematics tutorials in simple and native language so that you can get it easily |
#MathsMadeEasy is a channel where you can improve your #Mathematics |
This is an education channel where maths made easy will try to solve your problems |
Students may send the problems they are facing through comments |
Introduction
In this unit, we will prove theorems and their converses, if
any, about right bisector of a line segment and bisector of an angle.
But before that it will be useful to recall the following definitions:
Right Bisector of a Line Segment
A line is called a right bisector of a line segment if it is perpendicular
to the line segment and passes through its midpoint.
Bisector of an Angle
A ray BP is called the bisector of ∠ABC, if P is a point in the
interior of the angle and m∠ABP = m∠PBC.
Theorem 12.1.1
Any point on the right bisector of a line
segment is equidistant from its end points.
Given
A line LM intersects the line segment AB at
the point C. Such that LM is perpendicular to AB and AC ≅ BC. P is a point on LM.
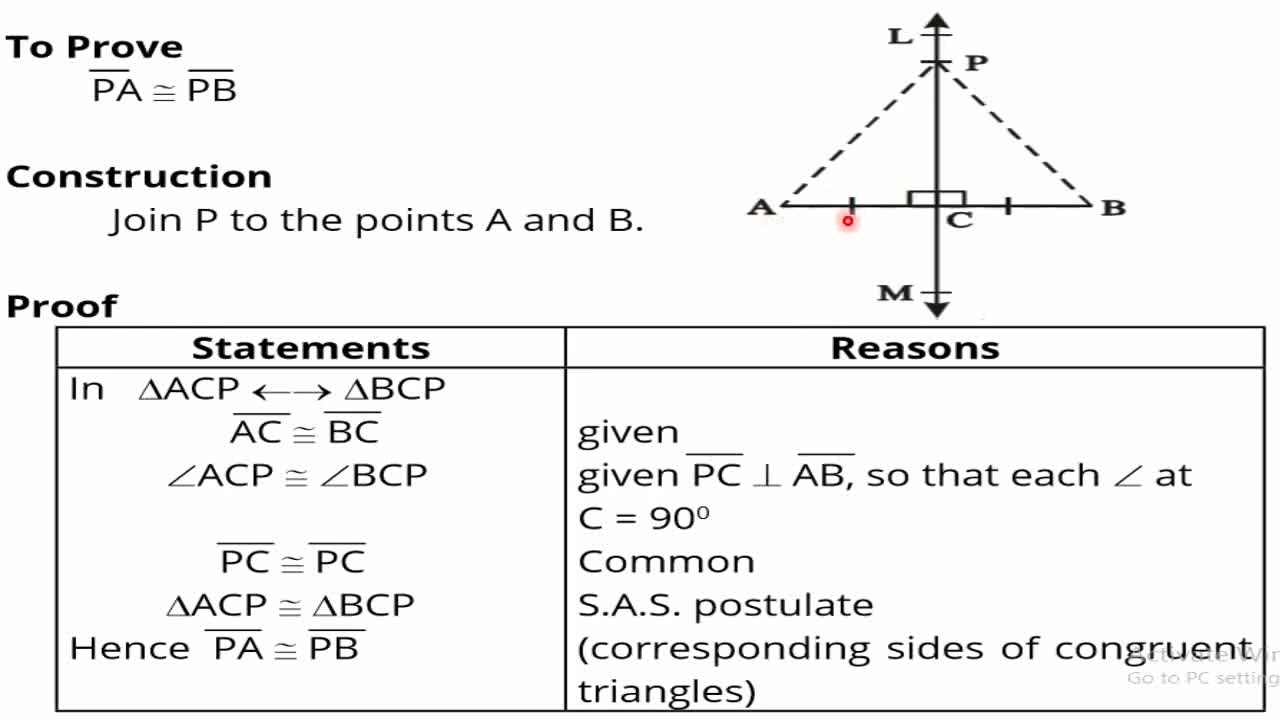
To Prove
PA ≅ PB
Construction
Join P to the points A and B.
Proof:
In ∆ACP ←→ ∆BCP
AC ≅ BC (given)
∠ACP ≅ ∠BCP (given PC is perpendicular to AB, so that each ∠ at
C = 90^0)
PC ≅ PC (Common
∆ACP ≅ ∆BCP (S.A.S. postulate)
Hence PA ≅ PB (corresponding sides of congruent triangles)
In this unit we stated and will proved the following theorems:
• Any point on the right bisector of a line segment is equidistant
from its end points.
• Any point equidistant from the end points of a line segment is on
the right bisector of it.
• The right bisectors of the sides of a triangle are concurrent.
• Any point on the bisector of an angle is equidistant from its arms.
• Any point inside an angle, equidistant from its arms, is on the bisector of it.
The bisectors of the angles of a triangle are concurrent.
• Right bisection of a line segment means to draw a perpendicular
at the mid point of line segment.
• Bisection of an angle means to draw a ray to divide the given
angle into two equal parts.
Mathematics (FBISE) |
Lecture # |
Unit #12 |
Theorem #12.1.1 |
Mathematics Science group |
Any point on the right bisector of a line segment is equidistant from its end points |
Dear viewers, it is my pleasure to deliver you mathematics tutorials in simple and native language so that you can get it easily |
#MathsMadeEasy is a channel where you can improve your #Mathematics |
This is an education channel where maths made easy will try to solve your problems |
Students may send the problems they are facing through comments |
Introduction
In this unit, we will prove theorems and their converses, if
any, about right bisector of a line segment and bisector of an angle.
But before that it will be useful to recall the following definitions:
Right Bisector of a Line Segment
A line is called a right bisector of a line segment if it is perpendicular
to the line segment and passes through its midpoint.
Bisector of an Angle
A ray BP is called the bisector of ∠ABC, if P is a point in the
interior of the angle and m∠ABP = m∠PBC.
Theorem 12.1.1
Any point on the right bisector of a line
segment is equidistant from its end points.
Given
A line LM intersects the line segment AB at
the point C. Such that LM is perpendicular to AB and AC ≅ BC. P is a point on LM.
To Prove
PA ≅ PB
Construction
Join P to the points A and B.
Proof:
In ∆ACP ←→ ∆BCP
AC ≅ BC (given)
∠ACP ≅ ∠BCP (given PC is perpendicular to AB, so that each ∠ at
C = 90^0)
PC ≅ PC (Common
∆ACP ≅ ∆BCP (S.A.S. postulate)
Hence PA ≅ PB (corresponding sides of congruent triangles)
In this unit we stated and will proved the following theorems:
• Any point on the right bisector of a line segment is equidistant
from its end points.
• Any point equidistant from the end points of a line segment is on
the right bisector of it.
• The right bisectors of the sides of a triangle are concurrent.
• Any point on the bisector of an angle is equidistant from its arms.
• Any point inside an angle, equidistant from its arms, is on the bisector of it.
The bisectors of the angles of a triangle are concurrent.
• Right bisection of a line segment means to draw a perpendicular
at the mid point of line segment.
• Bisection of an angle means to draw a ray to divide the given
angle into two equal parts.
Комментарии
 0:55:10
0:55:10
 0:15:45
0:15:45
 0:11:46
0:11:46
 0:00:29
0:00:29
 0:09:05
0:09:05
 0:08:36
0:08:36
 0:08:06
0:08:06
 0:11:38
0:11:38
 0:00:21
0:00:21
 0:07:27
0:07:27
 0:38:54
0:38:54
 0:12:26
0:12:26
 0:06:27
0:06:27
 0:07:28
0:07:28
 0:42:03
0:42:03
 0:15:31
0:15:31
 0:10:51
0:10:51
 0:05:15
0:05:15
 0:12:57
0:12:57
 1:12:13
1:12:13
 0:10:01
0:10:01
 0:12:42
0:12:42
 0:08:19
0:08:19
 0:01:14
0:01:14