filmov
tv
Limit with 0^0 form but multivariable version
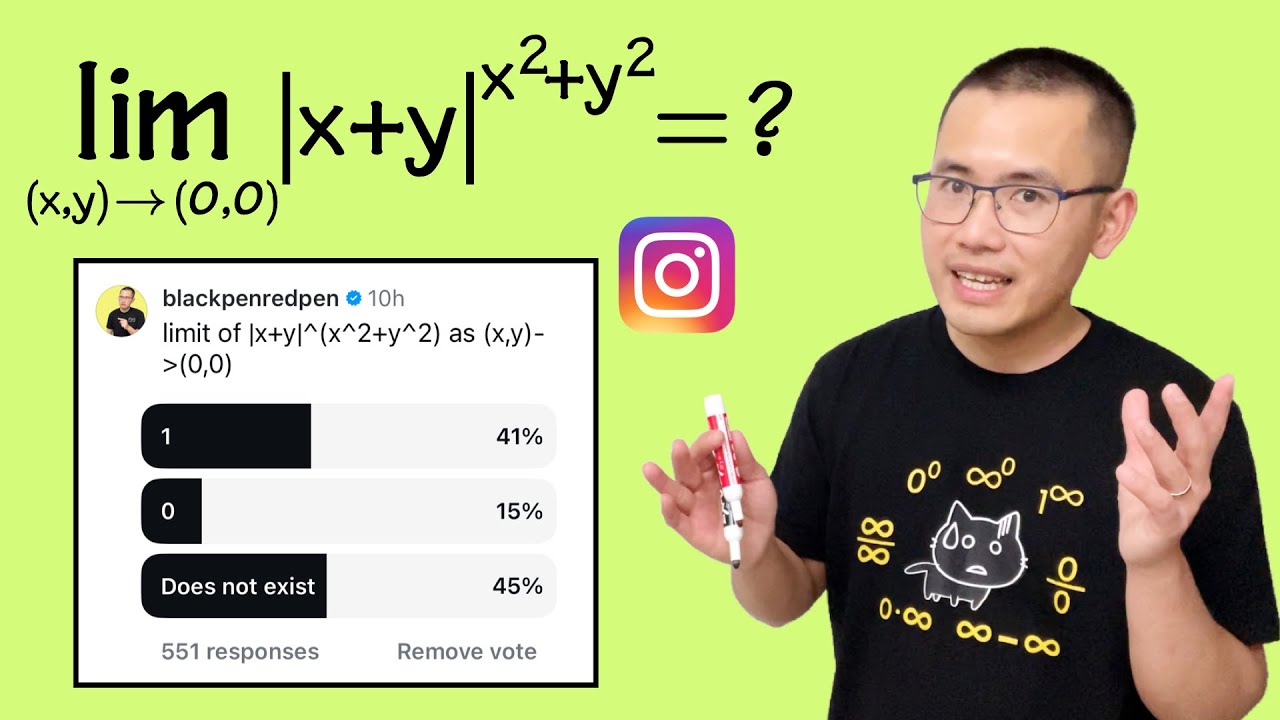
Показать описание
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Limit of [0/0] Indeterminate Form
A cute limit with 0^0 form and the answer is 0
Evaluating Limits By Factoring
Limits in Indeterminate Form (Part 1) - Factoring
How to Find Any Limit (NancyPi)
Indeterminate Forms
This is a very famous limit
#GeeklyHub How To Solve 0/0 Limit Problem?
Master L'Hospital Rule, Compute limit of indeterminate forms of the type 0^0
Infinite Limits and Vertical Asymptotes
Compute limits involving trig functions without L'Hôpital's rule | Step-by-step explanatio...
Solve limit that equal to 0/0 (indeterminate form)
L'Hopital's Rule for the 0/0 Indeterminate Form (proof)
I Finally Found Out What 0/0 Should Be
Limits L6 | Solving 1^infinity, 0^0, infinity^0 forms | #jee2024 #jee2025 #sameerchincholikar
Using L'Hospital's Rule with Indeterminate form Infinity^0
L'hopital's rule
What are Indeterminate forms ? | Meaning of 0/0 | Difference between Undefined and indeterminate
Indeterminate: the hidden power of 0 divided by 0
Solving Limits Mentally #calculus #limit #infinity #rational
Limits of Rational Functions - Fractions and Square Roots
How do you find the limit of the indeterminate form 0/0, ∞/∞, (-∞)/∞, ∞/(-∞), (-∞)/(-∞)? L'Hop...
Non-Zero Over Zero Limit
Important Results of (0/0) Form (Part-1) - Limits and Derivatives | Class 11 Maths CH 12 (2023-24)
Комментарии
![Limit of [0/0]](https://i.ytimg.com/vi/SHp7a9AgI6E/hqdefault.jpg) 0:08:51
0:08:51
 0:10:42
0:10:42
 0:11:35
0:11:35
 0:07:51
0:07:51
 0:16:42
0:16:42
 0:07:31
0:07:31
 0:00:48
0:00:48
 0:03:42
0:03:42
 0:03:38
0:03:38
 0:29:04
0:29:04
 0:10:19
0:10:19
 0:03:20
0:03:20
 0:09:20
0:09:20
 0:04:40
0:04:40
 1:15:37
1:15:37
 0:06:52
0:06:52
 0:13:09
0:13:09
 0:08:02
0:08:02
 0:12:33
0:12:33
 0:01:00
0:01:00
 0:10:06
0:10:06
 0:12:37
0:12:37
 0:00:50
0:00:50
 0:11:11
0:11:11