Cracking A Very Interesting Cubic Equation in Two Ways

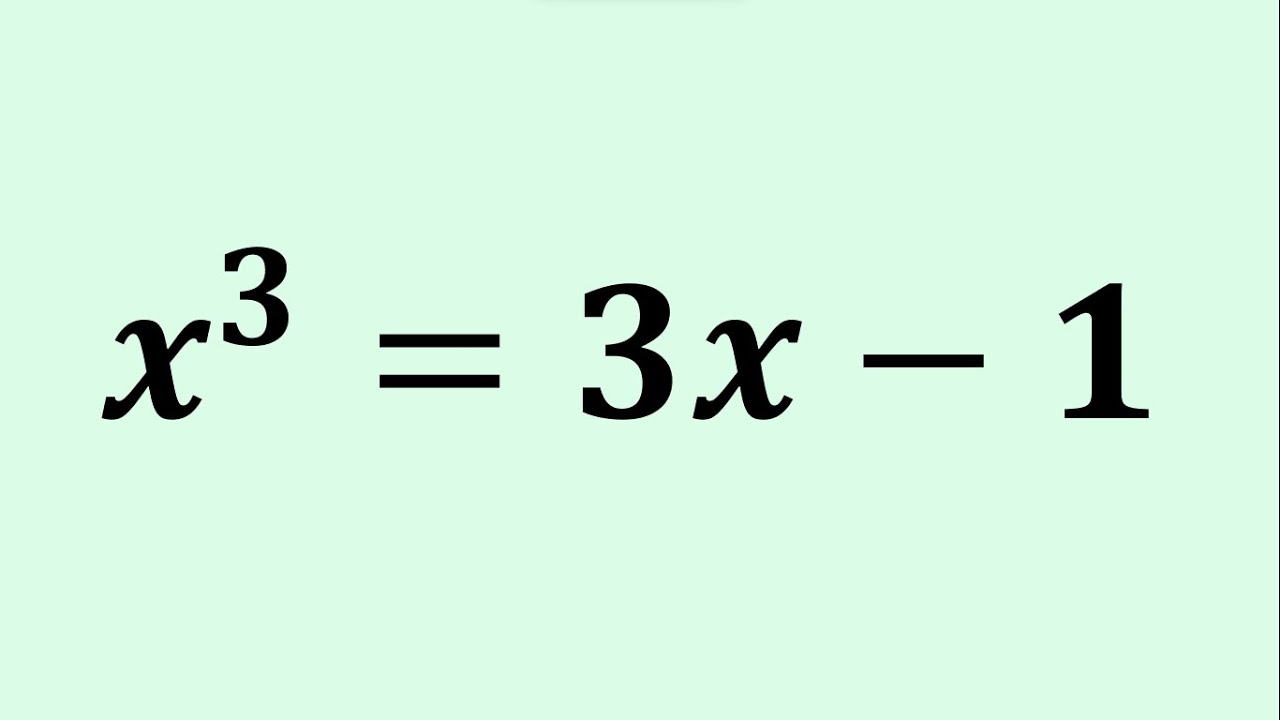
Показать описание

Cracking A Very Interesting Cubic Equation in Two Ways

Embark on a mathematical journey like never before with our latest YouTube video, "Cracking A Very Interesting Cubic Equation in Two Ways." 🧩📐 Join us as we delve into the heart of a truly fascinating cubic equation, navigating through two distinct methods of cracking its code. This isn't just a tutorial; it's an exploration into the beauty and complexity of mathematical problem-solving. Unlock the secrets, unravel the mysteries, and elevate your understanding of cubic equations like never before! 🔐🌐✨

Topics covered:
Algebra Challenge
Cubic equation
Trigonometry
Trig identities
General Solutions
Cardano's Formula
How to solve Cubic Equation using Cardano's method?
Math Olympiad
Algebra
Math Tricks
Algebraic identities
Algebraic manipulations
Substitution
Real solutions
Cubic equations
Quadratic formula
Quadratic equations
Polynomial
Algebraic Challenging Equations
Cubic equations
Math Olympiad Preparation

Timestamps:
0:00 Introduction
0:28 Method-1 (Trigonometric substitution)
0:52 Substitution
2:05 Trig identities
2:51 General solutions
6:45 Method-2 (Formula method)
9:02 Solving cubic equation using formula
13:09 Solutions

#Mathematics #CardanosMethod #CubicEquations #Algebra #MathTutorial #MathEducation #MathEnthusiast #SolvingPolynomials #EducationalVideo #LearnMath #MathematicsExplained #STEMeducation #CardanosFormula #MathGeek #ProblemSolving #MathematicalSkills #algebra #polynomials #maths #trigonometry #trigonometricequations

Don't forget to subscribe and hit that notification bell to stay updated and smash that like button!

We'd love to hear from you! Did you manage to solve the equation? What other math problems would you like us to cover? Let us know in the comments below!

🎓 Happy learning, and see you in the next video! 🎉

Thanks for Watching !!
@infyGyan