filmov
tv
Inertial and Non-Inertial Frames - The Equivalence Principle

Показать описание
Here (GR - 02), we venture into thinking about Inertial Frames of Reference - without the complication of very high velocities near to the speed of light. Then, still at relatively low velocities, we take a first simple look at Non-Inertial (or accelerating) Frames of Reference, in order to consider the way in which results from experiments seem to be modified when such Frames of Reference are used. This leads to a simplistic statement of the Equivalence Principle - its connection with idea of Inertial and Gravitational Mass, and also the idea that ‘gravity can bend light’. Finally, Newton’s basic equations are further manipulated to leave us with an equation for the divergence of a gravitational field ……. an equation which will be most useful later in the final formulation of Einstein’s Field equations (in GR - 19).
This video is part of a series of videos on General Relativity (GR-01 to GR-20), which has been created to help someone who knows a little bit about “Newtonian Gravity” and “Special Relativity” to appreciate both the need for “General Relativity”, and for the way in which the ‘modelling’ of General Relativity helps to satisfy that need – in the physics sense.
The production of these videos has been very much a ‘one man band’ from start to finish (‘blank paper’ to ‘final videos’), and so there are bound to be a number of errors which have slipped through. It has not been possible, for example, to have them “proof-watched” by a second person. In that sense, I would be glad of any comments for corrections ……. though it may be some time before I get around to making any changes.
By ‘corrections and changes’ I clearly do not mean changes of approach. The approach is fixed – though some mistakes in formulae may have been missed in my reviewing of the final videos, or indeed some ‘approximate explanations’ may have been made which were not given sufficient ‘qualification’. Such changes (in formulae, equations and ‘qualifying statements’) could be made at some later date if they were felt to be necessary.
This video (and channel) is NOT monetised
This video is part of a series of videos on General Relativity (GR-01 to GR-20), which has been created to help someone who knows a little bit about “Newtonian Gravity” and “Special Relativity” to appreciate both the need for “General Relativity”, and for the way in which the ‘modelling’ of General Relativity helps to satisfy that need – in the physics sense.
The production of these videos has been very much a ‘one man band’ from start to finish (‘blank paper’ to ‘final videos’), and so there are bound to be a number of errors which have slipped through. It has not been possible, for example, to have them “proof-watched” by a second person. In that sense, I would be glad of any comments for corrections ……. though it may be some time before I get around to making any changes.
By ‘corrections and changes’ I clearly do not mean changes of approach. The approach is fixed – though some mistakes in formulae may have been missed in my reviewing of the final videos, or indeed some ‘approximate explanations’ may have been made which were not given sufficient ‘qualification’. Such changes (in formulae, equations and ‘qualifying statements’) could be made at some later date if they were felt to be necessary.
This video (and channel) is NOT monetised
Комментарии
 0:00:28
0:00:28
 0:05:13
0:05:13
 0:04:38
0:04:38
 0:07:10
0:07:10
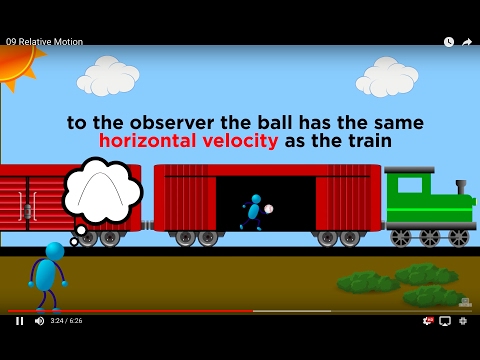 0:06:27
0:06:27
 0:01:22
0:01:22
 0:08:48
0:08:48
 0:12:48
0:12:48
 0:18:56
0:18:56
 0:16:56
0:16:56
 0:11:01
0:11:01
 0:00:49
0:00:49
 0:00:21
0:00:21
 0:04:52
0:04:52
 0:18:50
0:18:50
 0:09:26
0:09:26
 0:11:34
0:11:34
 0:13:40
0:13:40
 0:17:20
0:17:20
 0:00:48
0:00:48
 0:45:23
0:45:23
 0:00:33
0:00:33
 0:14:23
0:14:23
 0:00:54
0:00:54