filmov
tv
Equation of A Line Through Two Points

Показать описание
⭐ Join this channel to get access to perks:
#shorts #shortsvideo #shortsyoutube
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
#shorts #shortsvideo #shortsyoutube
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
How To Find The Equation of a Line From a Graph | Algebra
How To Find The Equation of a Line Given Two Points
Find Equation of Line Perpendicular to a Line Through a Given Point
Equation of a Line Through a Point - Corbettmaths
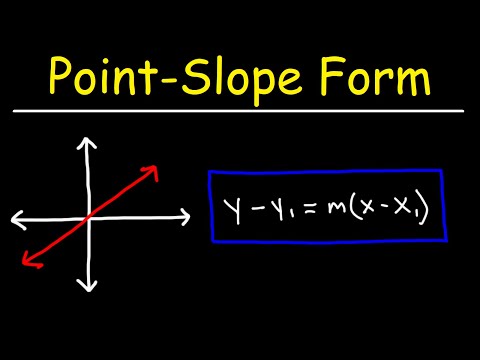
Write the equation of a line given a slope and a point the line runs through
Find the equation of a line through two points using slope intercept form
08 - The Point Slope Equation of a Line, Part 1 (Writing Equations of Lines)
Graphing Lines in Algebra: Understanding Slopes and Y-Intercepts
ACCUPLACER Math Test Prep (DAY 6) A bunch of function examples to feel confident on your exam!
How To Write The Equation of a Line Given The Slope and a Point | Algebra
Equation of a Line Given Two Points
Write the Equation of a Line Through Two Points
How To Find The Vector Equation of a Line and Symmetric & Parametric Equations
How to find the equation of a line given two points
10 - Writing Equations of Lines, Part 1 (Slope Intercept Form & Point Slope Form)
Find the equation of a line perpendicular to a line through a point
NECO 2020 Question 30 | Equation of a straight line
Finding the equation of a straight line given the gradient and a point
Equation of a Line Parallel to a Given Line Through a Point
GCSE Maths - Finding the Equation of a Straight Line From 2 Sets of Coordinates #69
Linear Equations - Algebra
Write the equation of a parallel line using point slope form
Point Slope Form - Basic Introduction - Algebra
Find the Equation of a Line Given Two Points
Комментарии
 0:10:05
0:10:05
 0:07:38
0:07:38
 0:02:26
0:02:26
 0:08:13
0:08:13
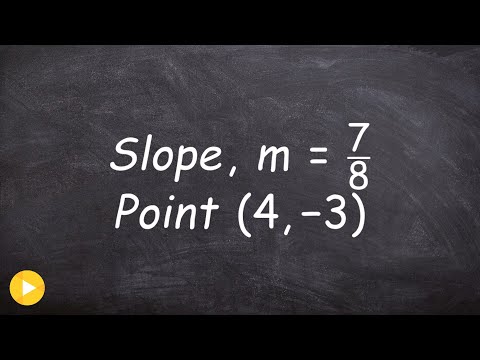 0:04:37
0:04:37
 0:05:04
0:05:04
 0:24:28
0:24:28
 0:06:52
0:06:52
 0:12:12
0:12:12
 0:08:32
0:08:32
 0:05:22
0:05:22
 0:07:50
0:07:50
 0:11:37
0:11:37
 0:04:41
0:04:41
 0:24:06
0:24:06
 0:02:49
0:02:49
 0:05:52
0:05:52
 0:01:54
0:01:54
 0:03:11
0:03:11
 0:06:07
0:06:07
 0:32:05
0:32:05
 0:05:25
0:05:25
 0:12:53
0:12:53
 0:04:38
0:04:38