filmov
tv
Chapter 04.10: Lesson: A Physical Example of Application of Eigenvalues and Eigenvectors

Показать описание
10 ICSE : Physics chapter 4 : Refraction at Plane Surfaces : Imporatnt Compilation
Class 9 - Physics - Chapter 4 - Lecture 1 - 4.1 & 4.2 - Allied Schools
Plus One Physics Christmas Exam | Laws of Motion | Full Chapter | Chapter 4 | Exam Winner +1
Physical Education and Sports for Children with Special Needs | One shot | Class 11 | Chapter 4
Class 9 - Physics - Chapter 4 - Lecture 10 - Numericals (4.1 to 4.3) - Allied Schools
Physical education and sports for CWSN | Unit 4 | Class 12 | Physical Education
PSEB 10th Class Physical Education September Paper 2024 || Full Solved Paper || 26-09-2024 #pseb
Enduring The Challenges|Start Here | Chapter 4
Physical education and sports for CWSN | Unit 4 | Class 12 | Physical education
PE & Sports for CWSN Oneshot Unit 4 Physical Education Class 12 CBSE 2023-24 Board Papa series 🔥...
12th Physics | Chapter 4 | Thermodynamics | Lecture 1 | Maharashtra Board |
Physical Education And Sports for Cwsn class11 / One Shot🔥 / Animation / Chapter4 P.E / Cbse 2024-25...
Chapter 4 numericals class 11 physics | physics ka safar
Class 9 - Physics - Chapter 4 - Lecture 3 - 4.4 & 4.5 - Allied Schools
Class 10 - Physics - Chapter 13 - Lecture 1 - 13.1 Production of Electric Charge - Allied Schools
Refraction of Light at Plane Surfaces Class 10 ICSE | Refraction of Light One Shot |@sirtarunrupani
Acids Bases and Salts
LANDFORMS | Types Of Landforms | Landforms Of The Earth | The Dr Binocs Show | Peekaboo Kidz
The Periodic Table: Crash Course Chemistry #4
VERY IMP PROBLEMS IN REFRACTION 04 || CLASS 10 || REFRACTION OF SPHERICAL SURFACES
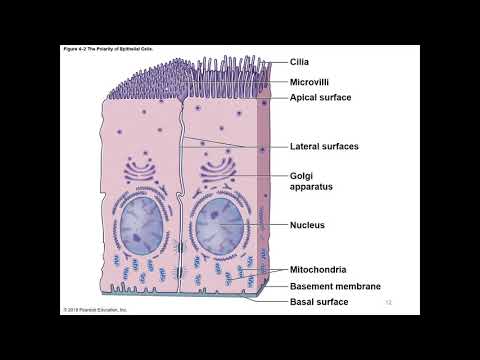
Chapter 4 The Tissue Level of Organization
Carbon and its Compounds - One shot🔥| Class 10 Boards| Full Chapter Science|
Class 9 - Physics - Chapter 4 - Lecture 2 - 4.3 Resolution of Forces - Allied Schools
11 Chap 4 | Chemical Bonding and Molecular Structure 01| Introduction | Cause of Chemical Bonding |
Комментарии
 0:52:36
0:52:36
 0:09:45
0:09:45
 1:49:38
1:49:38
 0:25:12
0:25:12
 0:15:40
0:15:40
 0:32:41
0:32:41
 0:19:12
0:19:12
 0:23:17
0:23:17
 0:19:58
0:19:58
 0:23:33
0:23:33
 0:23:09
0:23:09
 0:34:57
0:34:57
 0:49:05
0:49:05
 0:13:23
0:13:23
 0:17:06
0:17:06
 1:12:32
1:12:32
 0:17:58
0:17:58
 0:07:35
0:07:35
 0:11:22
0:11:22
 0:43:19
0:43:19
 1:29:51
1:29:51
 1:53:52
1:53:52
 0:11:35
0:11:35
 0:24:44
0:24:44