filmov
tv
Working With Algebraic Expressions
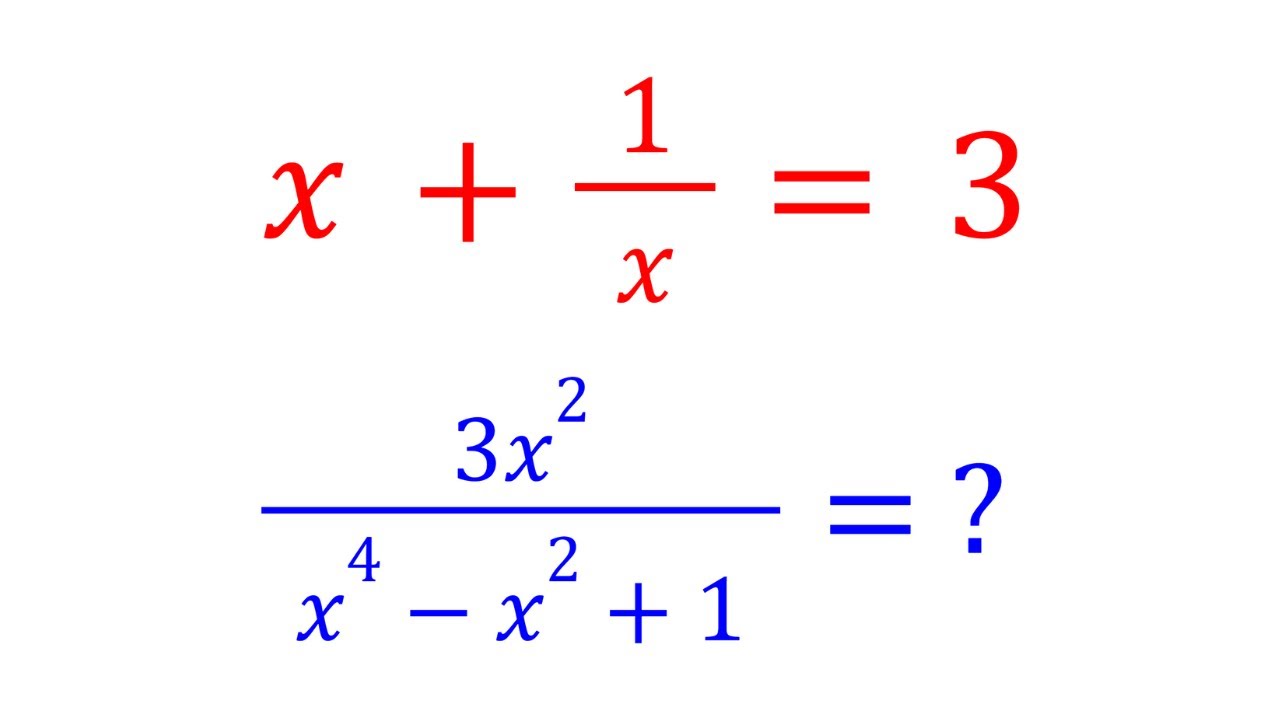
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials #algebraic
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials #algebraic
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Algebraic Expressions (Basics)
Simplifying Expressions / Collecting like terms / Algebra
Algebraic Expressions Made Easy: Learn How to Evaluate Them
Algebra Basics: What Is Algebra? - Math Antics
Simplifying Algebraic Expressions | Distributive Property & Combining Like Terms | Math with Mr....
Algebra Basics: Solving 2-Step Equations - Math Antics
How to Simplify an Expression: A Beginner's Guide | Algebraic Expressions | Math with Mr. J
GCSE Maths - How to Simplify Algebraic Expressions
Primary mathematics: Algebraic Expressions
Expanding Brackets
algebraic expressions working model with led lights - shorts | howtofunda
Grade 9 Algebraic Expressions
Introduction to Algebra: Using Variables
ALGEBRAIC EXPRESSIONS & EQUATIONS | GRADE 6
Algebra - How To Solve Equations Quickly!
algebraic expressions working model - maths tlm - #shorts - craftpiller
Writing Algebraic Expressions | Writing Expressions with Variables | Math with Mr. J
How to solve algebraic equations
Can you solve this equation?
🤔How to simplify algebraic expressions??? Algebraic Expressions/Short Tricks #shorts #shortsfeed
What are variables, expressions, and equations? | Introduction to algebra | Algebra I | Khan Academy
How to simplify an algebraic fraction using difference of two squares #sdgs
Algebra Basics: The Distributive Property - Math Antics
Algebra Formulas
Комментарии
 0:09:56
0:09:56
 0:00:06
0:00:06
 0:00:53
0:00:53
 0:12:07
0:12:07
 0:10:22
0:10:22
 0:10:29
0:10:29
 0:55:18
0:55:18
 0:06:27
0:06:27
 0:54:33
0:54:33
 0:00:51
0:00:51
 0:00:15
0:00:15
 0:09:14
0:09:14
 0:04:04
0:04:04
 0:20:45
0:20:45
 0:25:05
0:25:05
 0:00:06
0:00:06
 0:12:52
0:12:52
 0:01:01
0:01:01
 0:00:28
0:00:28
 0:00:16
0:00:16
 0:06:55
0:06:55
 0:00:51
0:00:51
 0:11:54
0:11:54
 0:00:05
0:00:05