filmov
tv
Gaussian Integral: Infinite Series Approach
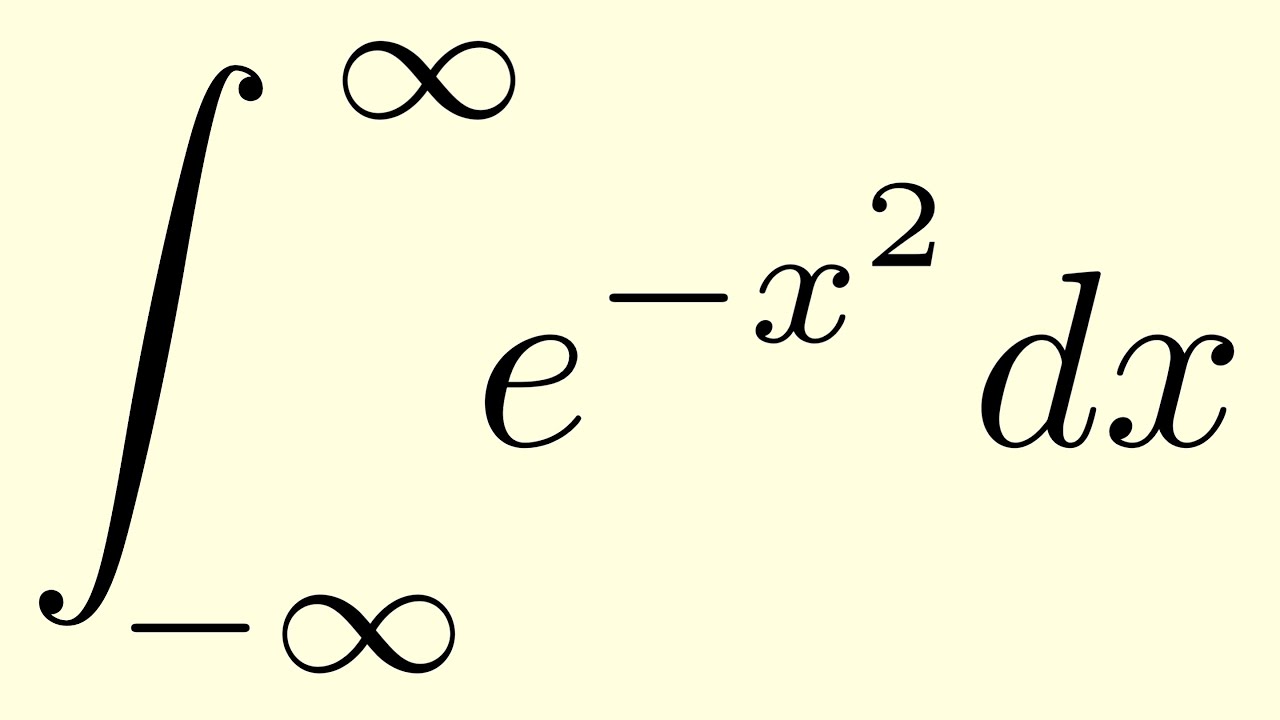
Показать описание
We evaluate the Gaussian integral, using an approach based on series expansions.
This argument can be traced back to a Stack Exchange post here:
Exchanging the order of summation and integration:
00:00 Setup
02:05 Infinite series
04:05 Integrating
08:03 Partial fractions
10:59 Simplifying the inner sum
14:15 Back to integration
17:45 Back to powers of e
21:23 Taking limits
This argument can be traced back to a Stack Exchange post here:
Exchanging the order of summation and integration:
00:00 Setup
02:05 Infinite series
04:05 Integrating
08:03 Partial fractions
10:59 Simplifying the inner sum
14:15 Back to integration
17:45 Back to powers of e
21:23 Taking limits
Комментарии