filmov
tv
Simplify the Cube Root of 27/16 =? Algebra Problem - MOST will NOT Get RIGHT!
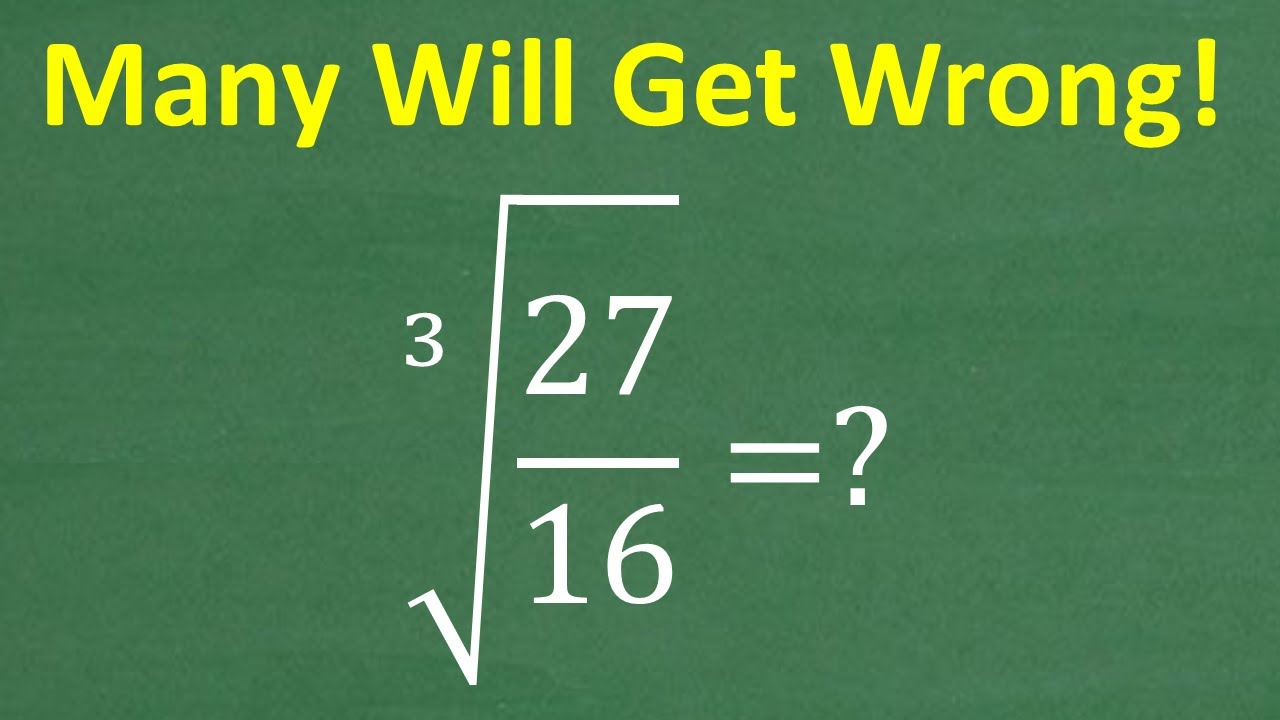
Показать описание
Help with Middle and High School Math
Test Prep for High School Math, College Math, Teacher Certification Math and More!
Popular Math Courses:
Math Foundations
Math Skills Rebuilder Course:
Pre-Algebra
Algebra
Geometry
Algebra 2
Pre-Calculus
• MIDDLE & HIGH SCHOOL MATH
• HOMESCHOOL MATH
• COLLEGE MATH
• TEST PREP MATH
• TEACHER CERTIFICATION TEST MATH
How to Simplify a Cube Root (Non-Perfect Cubes) | Simplifying Cube Roots | Math with Mr. J
How To Simplify Cube Roots
Simplify The Cube Root of an Expression
Learn How to Simplify the Cube Root of a Number, Cube Root(54)
How to Simplify a Cube Root
How to Simplify the Cube Root of a Fraction: cube root (27/64)
Simplifying cube roots | Exponent expressions and equations | Algebra I | Khan Academy
Simplify Cube Roots with Variables (not perfect cubes)
Learn How to Simplify the Cube Root of a Non Cube Number, Cube Root(16)
How to Simplify a Cube Root: - cube root (40)
Simplify the Cube Root Radical Expression. MOST will NOT Get RIGHT!
Learn how to simplify the cube root of an expression
Tutorial Simplify and Multiply the Cube Root of Two Numbers
Simplify the Cube Root of 120 over the Cube Root of 3
How to Simplify a CUBE ROOT - A Radical Expression with Variables
How to simplify a cube root using a factor tree
Simplifying a cube root | Exponents, radicals, and scientific notation | Pre-Algebra | Khan Academy
How to Simplify a Cube Root Using Prime Factorization (Non-Perfect Cubes) | Math with Mr. J
How to Simplify a Cube Root: cube root (343)
Simplify the Cube Root of 24
5 times the cube root of 192 = ? Simplify the Cube Root Radical Expression. MOST will NOT Get RIGHT!
Using prime factorization to simplify the cube root of an expression
How to Simplify A Cube Root Radical Expression
Simplify the Cube Root of 40
Комментарии
 0:04:12
0:04:12
 0:14:12
0:14:12
 0:06:20
0:06:20
 0:01:51
0:01:51
 0:06:15
0:06:15
 0:00:20
0:00:20
 0:05:25
0:05:25
 0:04:10
0:04:10
 0:01:35
0:01:35
 0:00:35
0:00:35
 0:18:13
0:18:13
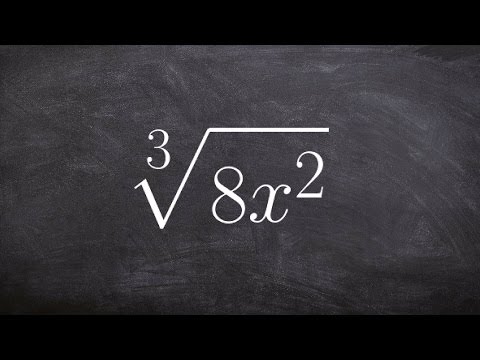 0:01:09
0:01:09
 0:02:16
0:02:16
 0:09:41
0:09:41
 0:01:35
0:01:35
 0:05:30
0:05:30
 0:02:37
0:02:37
 0:05:37
0:05:37
 0:00:34
0:00:34
 0:01:36
0:01:36
 0:09:25
0:09:25
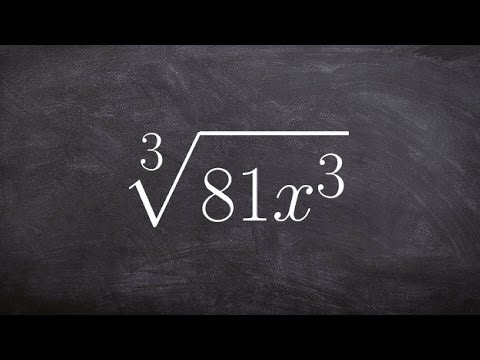 0:01:43
0:01:43
 0:02:35
0:02:35
 0:05:23
0:05:23