filmov
tv
This question frightened 500K+ examinees!
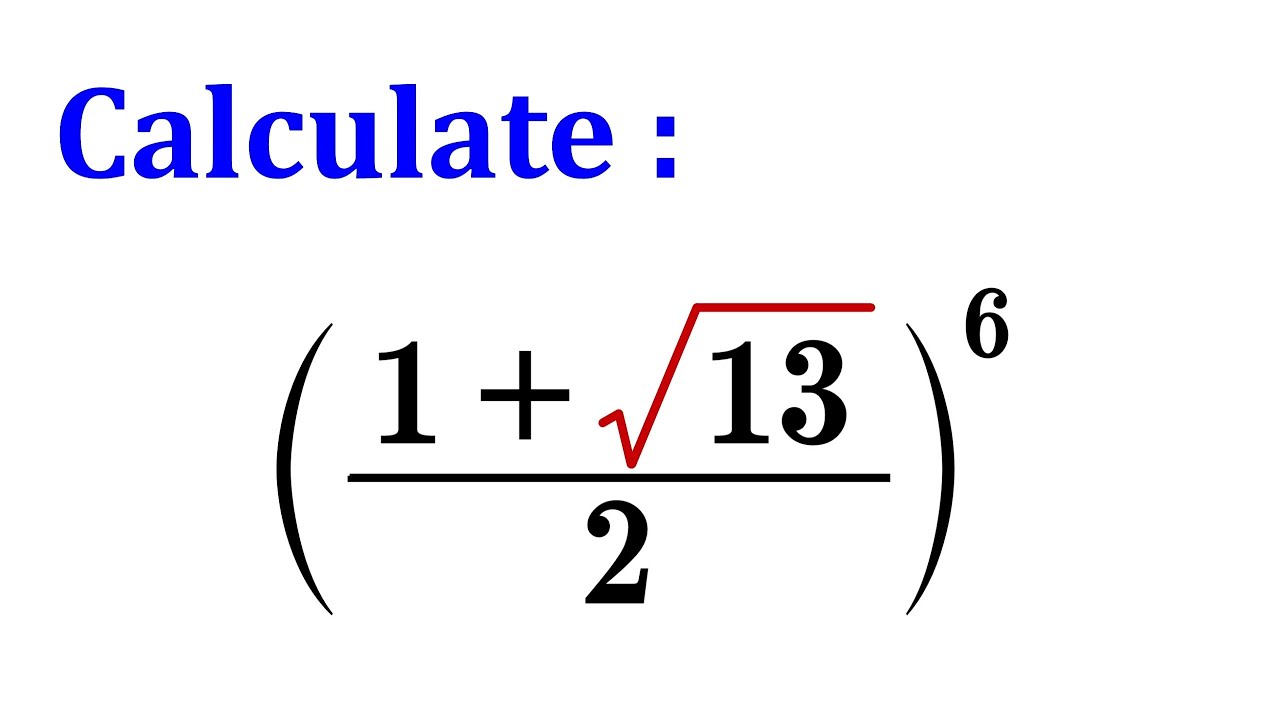
Показать описание
How do you solve this equation? Use this fanatic trick!
Russian Math Question|it frightened 500K + examinees!
I have bound a god-level exclusive talent, which can raise the skill level cap to god level!
I Grow Stronger by Killing Any Creature.After Rebirth, I Bought a Million Mosquitoes and Killed Them
Who says I'm a weak summoner? I can gain no-cooldown skills and summon a shadow legion!
I have awakened nine SSS-level talents. With just one skill, Blue Star might explode- Manhwa Recap
I Awakened a SSS Hidden Class, Gunner, Giving Me Unlimited Ammo and Automatic Headshot Targeting!
To cure my poisoned sister, I awakened a 3S-level ice-based superpower.
I Fed My Royal Beast Devil Fruits as Snacks, Instantly Turning It into a Divine Beast!
Public Speaking Anxiety Tips
I possess countless treasure chests that can yield anything, and my strength is skyrocketing.
Former CIA Officer Exposes The Shadow Government | Candace Ep 100
In This World,You Can Trade Lifespan for Anything,I Used 50 Years Just to Get a Roll of Toilet Paper
I Awakened the Weakest E Talent,But I Got an Attribute Point System That Upgraded My Talent to SSSSS
I Awakened a System That Multiplies Skills by 10000,Turning a Simple Fireball into a Forbidden Spell
The system provides me with a location-based check-in system to help me become a powerful villain.
Being A Necromancer With Godly Talent, I Have All My Skills Amplified 10x In The Level 1
LIVE ! Personal Injury Trial Attorney answers your FAQs: Welcome to RAW LAW - 7th of January 2025
This system is a bit weird! Even stones on the roadside can be used as nuclear bombs
With Each Monster a Man Kills, His Strength Goes up by 3. After Killing Nearly 9999999 Monsters.....
I was a useless college student, but after traveling to another world, I became a god of war.
In This World,You Can Trade Lifespan For Anything,I Used 50 Years Just To Get A Roll Of Toilet Paper
Monster Invasion: Hidden Class Unlocked, Immortal as Long as My Summons Live
After Awakening a Hidden Class, I Bound a System, That Can Fuse and Evolve Similar Beast Pets!
Transported to a realm of magic, I've bonded with mystical creatures who now fight for me.
Комментарии
 0:06:02
0:06:02
 8:36:27
8:36:27
 11:12:17
11:12:17
 9:28:28
9:28:28
 10:08:03
10:08:03
 13:37:59
13:37:59
 7:59:48
7:59:48
 12:25:00
12:25:00
 0:06:09
0:06:09
 8:40:33
8:40:33
 1:14:35
1:14:35
 16:13:21
16:13:21
 23:27:34
23:27:34
 9:37:16
9:37:16
 9:05:46
9:05:46
 21:01:32
21:01:32
 1:19:59
1:19:59
 13:12:47
13:12:47
 8:28:21
8:28:21
 8:07:32
8:07:32
 18:08:52
18:08:52
 10:59:35
10:59:35
 10:57:19
10:57:19
 10:33:59
10:33:59