filmov
tv
📚 Determine the volume of a parallelepiped

Показать описание
Follow us:
Q1. Find the volume of the parallelepiped determined by the
vectors a, b, and c.
What you'll need:
Scalar triple product formula:
• Volume of the parallelepiped is the absolute value of the one determinate obtained above. If the volume comes out as 0, then vectors must lie on the same plane (referred to as coplanar).
Parallelepiped formed by vectors, a, b, and c:
Q2. Use the scalar triple product to show that the vectors a=⟨1,4,−7⟩, b=⟨2,−1,4⟩, and c=⟨0,−9,18⟩ are coplanar.
 0:05:47
0:05:47
 0:09:12
0:09:12
 0:01:53
0:01:53
 0:01:32
0:01:32
 0:02:51
0:02:51
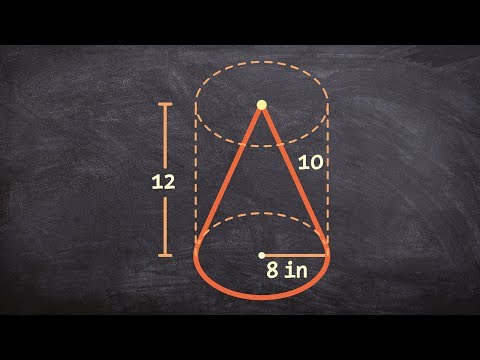 0:03:54
0:03:54
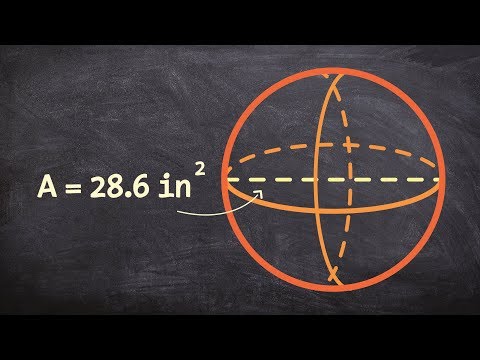 0:05:02
0:05:02
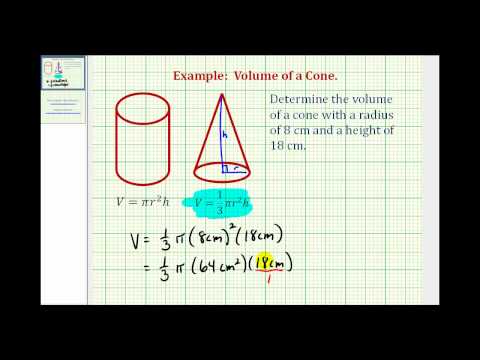 0:03:45
0:03:45
 1:08:19
1:08:19
 0:02:51
0:02:51
 0:01:15
0:01:15
 0:01:41
0:01:41
 0:05:06
0:05:06
 0:04:32
0:04:32
 0:02:36
0:02:36
 0:22:14
0:22:14
 0:05:28
0:05:28
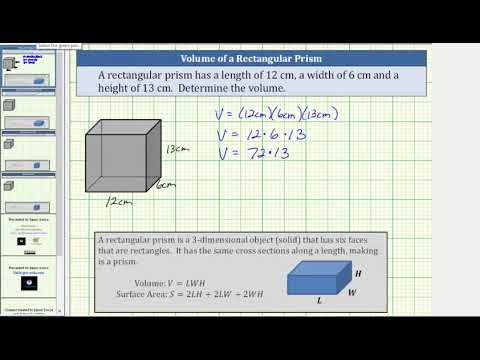 0:02:42
0:02:42
 0:09:48
0:09:48
 0:11:46
0:11:46
 0:04:31
0:04:31
 0:00:33
0:00:33
 0:02:04
0:02:04
 0:09:20
0:09:20