filmov
tv
CHEATING DEVELOPER vs Log n Engineer on Sqrt(x), Leetcode 69

Показать описание
FAANG Coding Interviews / Data Structures and Algorithms / Leetcode
CHEATING DEVELOPER vs Log n Engineer on Sqrt(x), Leetcode 69
CHEATING DEVELOPER vs Log n Engineer on Sqrt(x), Leetcode 69
Is This Considered Cheating?#shorts #airsoft
Fake hacker vs real hacker #roblox #shorts
Boy Ignore Girl 😎 || Don't Underestimate Boys 😦 || Boys Attitude 🔥||Attitude Status😈#viral #sho...
Candidate Sets Up Hidden Cameras to Cheat During Online Exam
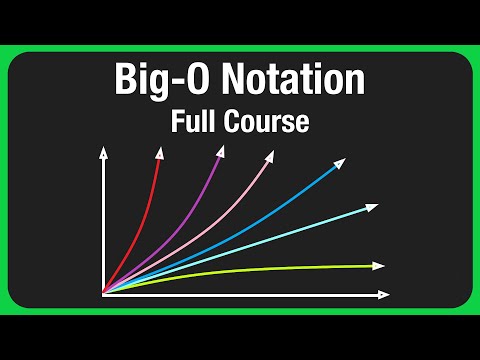
Big-O Notation - For Coding Interviews
Real code 💥 Indian bike driving 3d all new cheat code update + plugin cheat code #shorts #gaming
I Generated 4 Billions Steam Keys
Kid got banned for being racist on roblox. @gloomstygian
PlayStation Cheat Code You've Never Heard Of 🤯
Top 10 Countries With Most Powerful Hacker In The World. #shorts
ILLEGAL Move & WIN the Game! #shorts
Steroid Or No Steroid? Reviewing Physiques Of International Stars With Ronnie Coleman #shorts
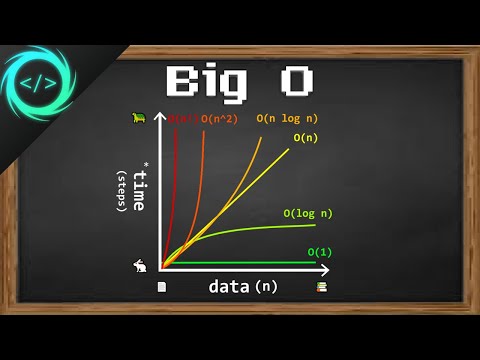
Learn Big O notation in 6 minutes 📈
Who Is The Worst Minecraft Player?
I Became A Epic Employee 😲
How To BAN Anyone Who Swears on Roblox😱
BEST ROBLOX Dead Rails Script in 2025! 🚂💥
Stealing Most Rare BRAINROT Worth 10M 💰💰💰
Marshmallow Squid Game: will it work? ✅ or not ❌
Roblox Troll Tower SECRET Entry 😱
FINALLY REAL MULTIPLAYER MODE CHEAT CODE 🔥🤑|| INDIAN BIKE DRIVING 3D #indianbikedriving3d #shorts...
hidden menu on the xbox series x/s
Комментарии
 0:00:59
0:00:59
 0:00:59
0:00:59
 0:00:14
0:00:14
 0:00:25
0:00:25
 0:00:29
0:00:29
 0:00:23
0:00:23
 0:20:38
0:20:38
 0:00:05
0:00:05
 0:00:33
0:00:33
 0:00:18
0:00:18
 0:00:10
0:00:10
 0:00:29
0:00:29
 0:00:35
0:00:35
 0:00:53
0:00:53
 0:06:25
0:06:25
 0:00:33
0:00:33
 0:00:25
0:00:25
 0:00:33
0:00:33
 0:00:12
0:00:12
 0:00:16
0:00:16
 0:00:14
0:00:14
 0:00:18
0:00:18
 0:00:21
0:00:21
 0:00:19
0:00:19