filmov
tv
How is the Circum-Radius Related with Side Lengths of a Triangle Inscribed

Показать описание
Important Formula to relate circum-radius to side lengths of Triangle
Circumcenter of a triangle is the point of intersection of the right bisector of the three sides of a triangle. All the three vertices are same distance away from the circumcentre and so a circle can be drawn circumscribing the triangle using this point as the centre.
Orthocentre of a triangle is a point where the perpendiculars drawn from each vertex to the opposite sides intersect. For an acute angle triangle the orthocenter is inside the triangle; for right triangle it is on the hypotenuse and for the obtuse angle triangle it lies outside the triangle.
Incentre of a triangle is the point of intersection of three interior angles of a triangle. A circle inscribed in a triangle can be drawn with center at the incenter.
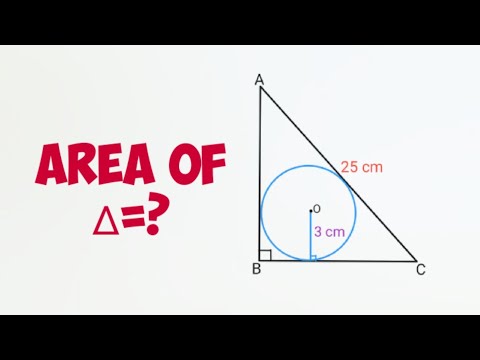
Area of triangle is semiperimeter times inradius.
#circumcenter #incenter #orthocenter #coordinategeometry #analyticalgeometry #mpm2d #rightbisector #anilkumar #mpm2d
Circumcenter of a triangle is the point of intersection of the right bisector of the three sides of a triangle. All the three vertices are same distance away from the circumcentre and so a circle can be drawn circumscribing the triangle using this point as the centre.
Orthocentre of a triangle is a point where the perpendiculars drawn from each vertex to the opposite sides intersect. For an acute angle triangle the orthocenter is inside the triangle; for right triangle it is on the hypotenuse and for the obtuse angle triangle it lies outside the triangle.
Incentre of a triangle is the point of intersection of three interior angles of a triangle. A circle inscribed in a triangle can be drawn with center at the incenter.
Area of triangle is semiperimeter times inradius.
#circumcenter #incenter #orthocenter #coordinategeometry #analyticalgeometry #mpm2d #rightbisector #anilkumar #mpm2d
How is the Circum-Radius Related with Side Lengths of a Triangle Inscribed
Area circumradius formula proof | AIME | Math for fun and glory | Khan Academy
Circumradius and Area of Triangle — Find Radius of Circumscribed Circle Using Area and Sides
circumradius of a sclene triangle 👌🥇
Can you find the circumradius ?
How to Calculate the Circumference of a Circle
In-radius & Circum-radius of Equilateral Triangle || Equilateral Triangle Inradius and Circumrad...
Circum Radius from Properties of triangle
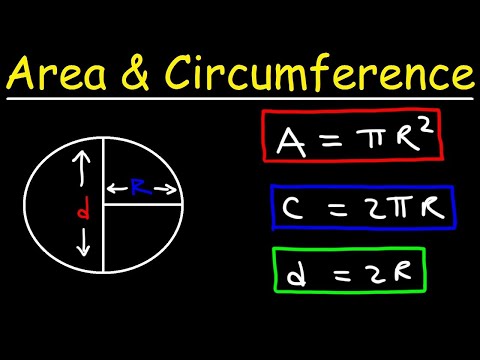
Circles - Area, Circumference, Radius & Diameter Explained!
#shorts how to find inradius and circum radius of triangle, incircle, circum circle concepts for ssc
Math Antics - Circles, Circumference And Area
Right angle triangle| inradius and circumradius| area of triangle| geometry| @logicxonomy
Animated proof of Inradius Area Formula
Geometry: How to find the circumradius of a triangle given the measurement of the three sides.
Find The 𝗖𝗜𝗥𝗖𝗨𝗠𝗥𝗔𝗗𝗜𝗨𝗦 ?
Area of triangle| Inradius| circumradius| geometry| @logicxonomy| shorts
Circumradius| inradius| Circumradius and Inradius| Circumcircle and Incircle formula derivation
EQUILATERAL TRIANGLE | INCIRCLE | CIRCUMCIRCLE | @math-xy
🤯Find In-Radius and Circum Radius of Right Angle Triangle in SECONDS🤯 #shorts
Finding the Circumradius and Inradius of a Triangle
CAT Preparation - Geometry Question 08
circumradius and inradius, important question 2022 #ssc
Circumradius| inradius| Circumradius and Inradius| Circumcircle and Incircle formula derivation
radius of circumcircle
Комментарии
 0:12:23
0:12:23
 0:09:06
0:09:06
 0:04:08
0:04:08
 0:00:15
0:00:15
 0:02:52
0:02:52
 0:00:59
0:00:59
 0:00:40
0:00:40
 0:07:48
0:07:48
 0:17:20
0:17:20
 0:00:56
0:00:56
 0:07:56
0:07:56
 0:01:09
0:01:09
 0:00:31
0:00:31
 0:09:56
0:09:56
 0:01:49
0:01:49
 0:00:18
0:00:18
 0:01:01
0:01:01
 0:00:05
0:00:05
 0:00:45
0:00:45
 0:13:04
0:13:04
 0:05:55
0:05:55
 0:01:25
0:01:25
 0:00:47
0:00:47
 0:00:16
0:00:16