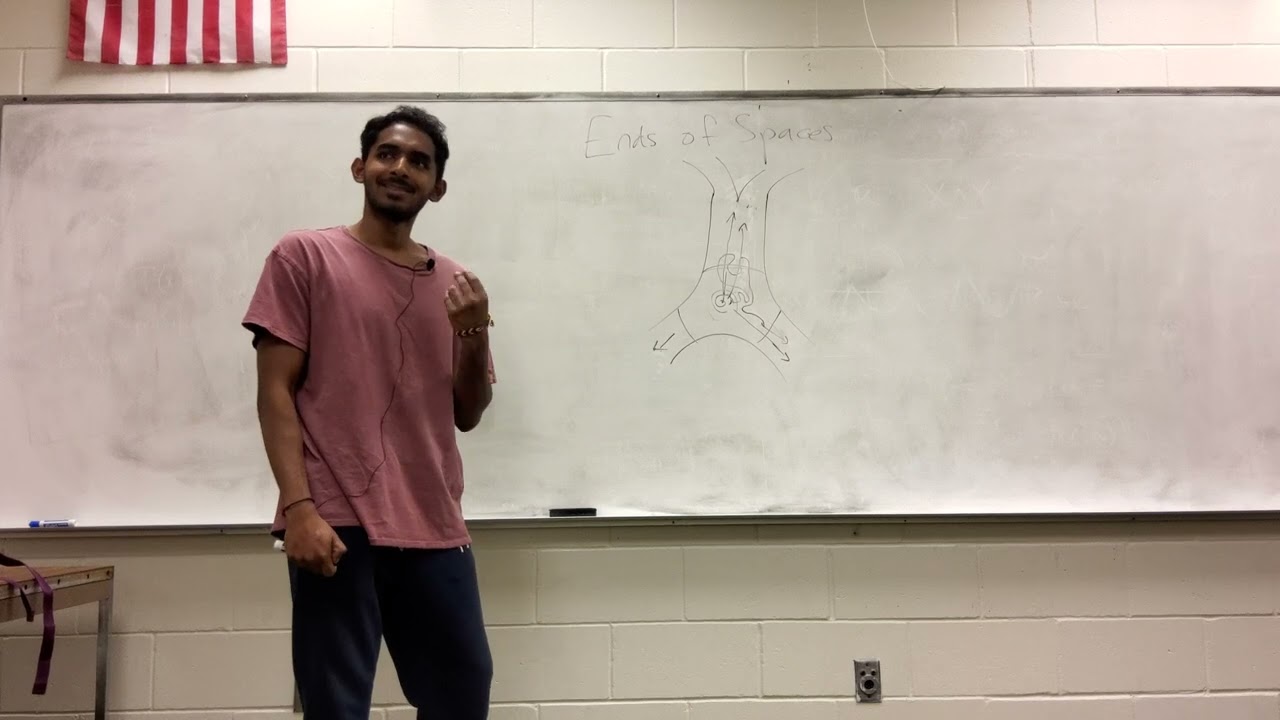
Ends of spaces

Hans Freudenthal first introduced the notion of the ends of a space in his PhD thesis in 1930. His motivation was in topological group theory. His notion of ends allowed him to associate to a given space, X, a set, the set of ends of X, which can be adjoined to X to compactify it. The set of ends were proven to be invariants under certain families of homeomorphisms of X after they are extended to homeomorphisms of the end compactification of X. This led to results such as: a path-connected topological group has no more than 2 ends. Since then, the notion of ends of a topological space has taken on a number of definitions, some not equivalent to others. The overarching motivation is always similar: compact spaces are nicer to study since their properties can be discerned using a finite amount of local information. Therefore, we wish to generate a functor from spaces to sets such that the set associated with a space is "created" (apologies for the vagueness) using complements of compact sets and allows us to study the space as imbedded in a bigger, compactified space. In Laymen's terms, we wish to formally define all the ways to reach "infinity" in a space. In this talk, I will lightly introduce the different notions of ends and their motivations. Time permitting, we can conclude by proving some major results.

-Panith Thiruvenkatasamy