30.2 Conditional Expectation, Part 1

preview_player
Показать описание
Motivation for conditional expectation, in a discrete setting. Relation to L^2 inner product.
  1. Todd Kemp
Рекомендации по теме
Conditional Expectation of 0:08:24

Conditional Expectation of Stock Prices Following a Binomial Tree

Conditional Expectation 0:07:51

Conditional Expectation

Lecture 26 Conditional 0:47:49

Lecture 26 Conditional Expectation + Sum of Two Random Variables

Module 3 2 0:22:36

Module 3 2 Conditional Expectations and Expected Value 1

Probability Adventures #16: 0:18:00

Probability Adventures #16: Conditional expectation

Conditional Expectation and 0:24:17

Conditional Expectation and Conditional Variance

Probability Tree and 0:39:22

Probability Tree and Conditional Expectation CFA Level 1 | Quants

Prediction lecture 2: 0:20:26

Prediction lecture 2: Approximating a conditional expectation

Find coveriance, coefficient 0:29:37

Find coveriance, coefficient of correlation, Conditional Expectation,Variance of Continuous r.v,

Ch04-3 Conditional Distributions 0:38:10

Ch04-3 Conditional Distributions (Part 1)

MA203, Lecture no28, 1:05:09

MA203, Lecture no28, Conditional Expectation 2.0 & Conditional Variance by Tapas Chatterjee, IIT

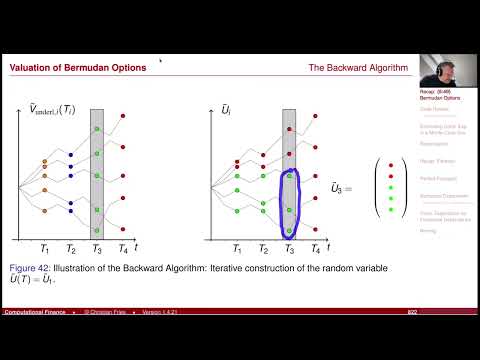
Lecture 2024-1 (42): 1:16:07

Lecture 2024-1 (42): Numerical Methods: American Monte-Carlo: Conditional Expectation in MC Sim(1/2)

Decision Analysis 1: 0:04:44

Decision Analysis 1: Maximax, Maximin, Minimax Regret

CFA Level I. 0:21:16

CFA Level I. Reading 9. Module 9 2 Conditional Expectations, Correlation

Conditional Probability And 0:35:09

Conditional Probability And Expectation

08-11. Conditional expectation 0:31:48

08-11. Conditional expectation - Main properties of the conditional expectation.

Introductory Econometrics and 0:24:37

Introductory Econometrics and Statistics | Conditional Distribution | Definition | Example | 30 |

CE01 Conditional Expectation 0:11:47

CE01 Conditional Expectation The Discrete Case Source

Probability Video 4.5: 0:25:40

Probability Video 4.5: Pairs of Random Variables - Conditional Expectation

Conditional Probability 0:37:03

Conditional Probability

Conditional Order Statistics 0:00:11

Conditional Order Statistics Numerical from Old Paper.

Conditional Expectation 0:09:58

Conditional Expectation

Abstract Bayes' Formula 0:35:34

Abstract Bayes' Formula and Conditional Expectation

08-01. Conditional expectation 0:31:14

08-01. Conditional expectation - Radon-Nikodym theorem and conditional expectation.

Комментарии
Автор

@0:53: There's a misstatement here. L^1(P_A) is NOT equal to L^1(P), unless P(A)=1 (in which case P_A = P). You can take any random variable that is L^1 on A and then set it equal to infinity on A^c; then it will be in L^1(P_A), but will not be in L^1(P). That's not a problem: the correct statement is that L^1(P) is CONTAINED in L^1(P_A), which is correct and easy to check from the formula for the integral with respect to P_A that is the content of this Lemma. That means that any L^1(P) random variable X is one for which E[X|A] makes sense, for all events A. (For any given event, E[X|A] makes sense fr some random variables that aren't in L^1(P), as described above, but since we want to string these together into a function that varies from one partition bin A to another, the best place to start is L^1(P), which is contained in all of the L^1(P_A).)

toddkemp-probability