filmov
tv
Finding the slope of tangent line using implicit differentiation

Показать описание
In this math example, we find the slope of a tangent line to our curve at a given point. To do so, we use implicit differentiation. The power rule is used whenever possible but we also need to use the product rule on this problem because we have one term that contains two variables. Each step of this process is explained as we proceed through them. Our derivative y' = dy/dx is isolated on one side of the equation by moving all terms that do not contain y' to the other side. Then we factor y' out of each term (as a common factor) and divide by the multiple on that side. The slope of the tangent line is then found by substituting in the given point for x and y in the derivative formula that we found. The solution is then simplified completely.
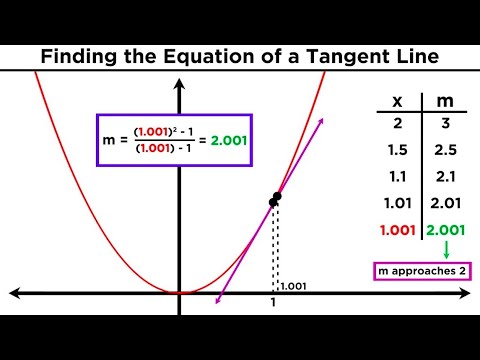 0:05:29
0:05:29
 0:02:01
0:02:01
 0:11:02
0:11:02
 0:04:24
0:04:24
 0:03:10
0:03:10
 0:12:40
0:12:40
 0:05:13
0:05:13
 0:04:39
0:04:39
 0:44:11
0:44:11
 0:15:43
0:15:43
 0:00:52
0:00:52
 0:04:37
0:04:37
 0:19:02
0:19:02
 0:08:28
0:08:28
 0:22:42
0:22:42
 0:08:36
0:08:36
 0:05:30
0:05:30
 0:00:14
0:00:14
 0:01:00
0:01:00
 0:00:39
0:00:39
 0:03:03
0:03:03
 0:06:55
0:06:55
 0:04:56
0:04:56
 0:03:29
0:03:29