Using Tan to Determine the Height of a Building

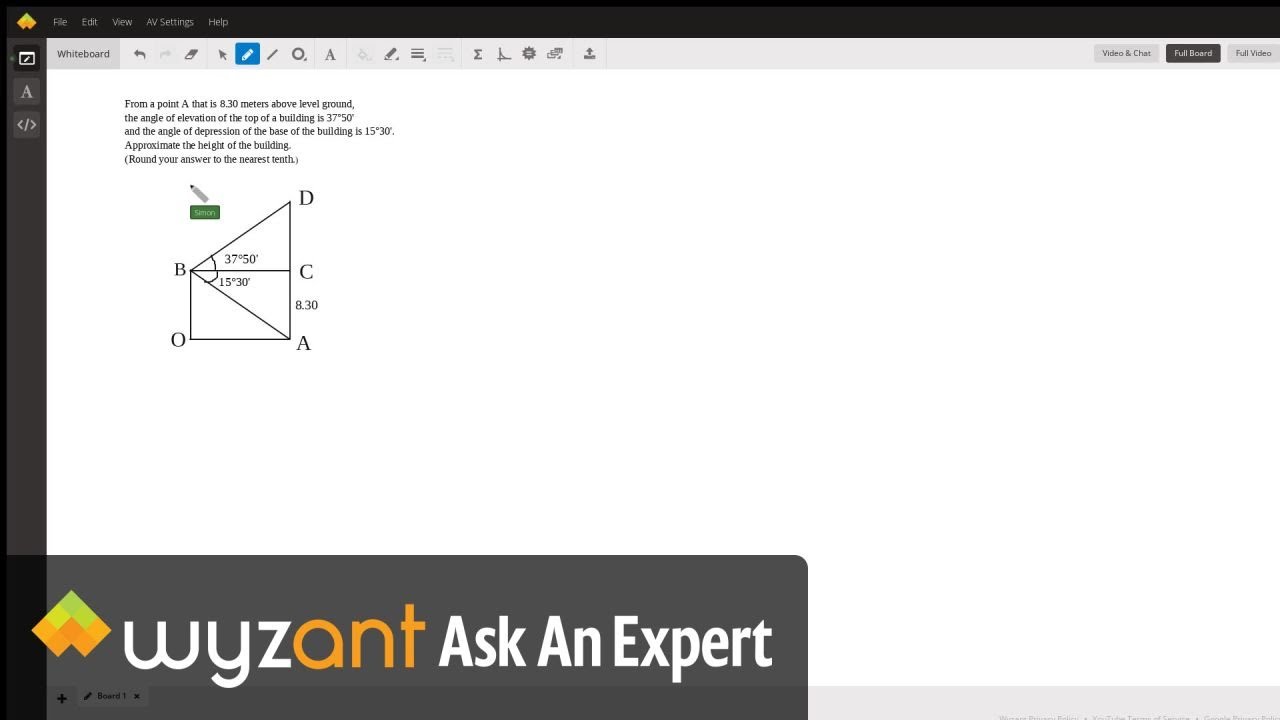
Question: From a point A that is 8.30 meters above level ground, the angle of elevation of the top of a building is 37°50'
and the angle of depression of the base of the building is 15°30'. Approximate the height of the building. (Round your answer to the nearest tenth.)

------------------------

Answered By:

Simon C.
Undergraduate Tutor Good at Simplifying Complex Concepts

------------------------

Written Explanation:

In this video I show how we can use the property of the tangent function, where tangent(angle) = opposite/adjacent, to determine the total height of the building.Written calculations (in case video doesn't process, I hope you can see my diagram):[EDIT: I forgot to convert the angle measurements to degrees, so the correct angle of elevation should be approximately 37.83 degrees and the angle of depression should be 15.5 degrees. My apologies for the confusion]Angle of Elevation: 37°50' = 37 + 50/60 ° = 37.83°Angle of Depression: 15°30' = 15 + 30/60 ° = 15.5°tan(15.5°) = 8.3 / BCBC = 8.3 / tan(15.5°)BC = 29.9tan(37.83°) = CD / BCCD = BC x tan(37.83°)CD = 29.9 x tan(37.83°)CD = 23.2Height = 8.30 + CD = 8.30 + 23.2 = 31.5 (rounded to nearest tenth)Again, my apologies for the confusion in the video.

------------------------

About: Wyzant Ask an Expert offers free answers to your toughest academic and professional questions from over 65,000 verified experts. It’s trusted by millions of students each month with the majority of questions receiving an answer within 1 hour of being asked. If you ever need more than just an answer, Wyzant also offers personalized 1-on-1 sessions with experts that will work with you to help you understand whatever you’re trying to learn.