filmov
tv
An Interesting Polynomial System

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #counting #geometry #numbertheory #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
An Interesting Polynomial System
An Interesting Polynomial System
An Interesting Polynomial System
An Interesting Polynomial System with Three Variables
Solving An Interesting Polynomial System in Two Ways
A Cool Polynomial System | Nice Graph!
A Nice Polynomial System
An Interesting Polynomial Equation
Class 10th Maths| PYQ SERIES | CHAPTER-2| POLYNOMIALS |PART- 6 | Most important questions of 2025
An Interesting Polynomial Equation
A Nice Polynomial System
Let's Solve A Nice Polynomial System
A Nice Polynomial System | Math Olympiads
A Nice Polynomial System
A Quick and Easy Polynomial System
A Polynomial System Inspired by Saratov Math Olympiads
Polynomial or not?🤔#shorts #maths.
A Quick and Easy Polynomial System
Relationship between zeros and coefficient of a polynomial #ncert #math #class10
Solving a Nice Polynomial System in Two Ways
Class 9 Math Chapter 2 Polynomial (Identity)
Solving A Polynomial System
Does the Polynomial Divide into the polynomial
Solving A Real Polynomial System in Two Ways
Комментарии
 0:09:27
0:09:27
 0:09:58
0:09:58
 0:16:30
0:16:30
 0:09:25
0:09:25
 0:12:01
0:12:01
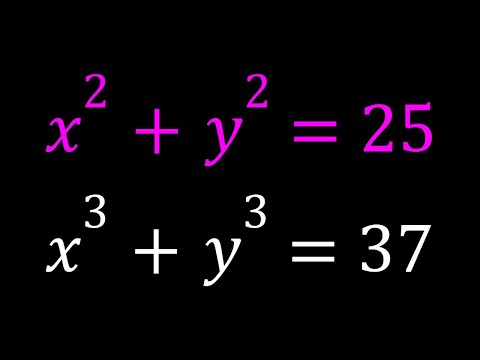 0:11:19
0:11:19
 0:08:40
0:08:40
 0:10:21
0:10:21
 0:08:46
0:08:46
 0:11:59
0:11:59
 0:08:13
0:08:13
 0:10:27
0:10:27
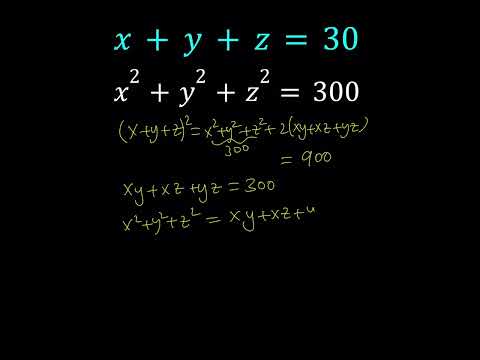 0:00:37
0:00:37
 0:08:19
0:08:19
 0:08:55
0:08:55
 0:09:04
0:09:04
 0:00:17
0:00:17
 0:09:13
0:09:13
 0:00:18
0:00:18
 0:09:27
0:09:27
 0:00:08
0:00:08
 0:03:11
0:03:11
 0:00:33
0:00:33
 0:10:59
0:10:59