Solving polynomial inequality that has negative multiple in front and interval notation

In this math example problem, we solve an already factored polynomial inequality that included a negative multiple in front to determine the intervals where the function will be greater than zero. The same process can be utilized for a similar problem where the function would be less than, less than or equal to, or greater than or equal to zero.

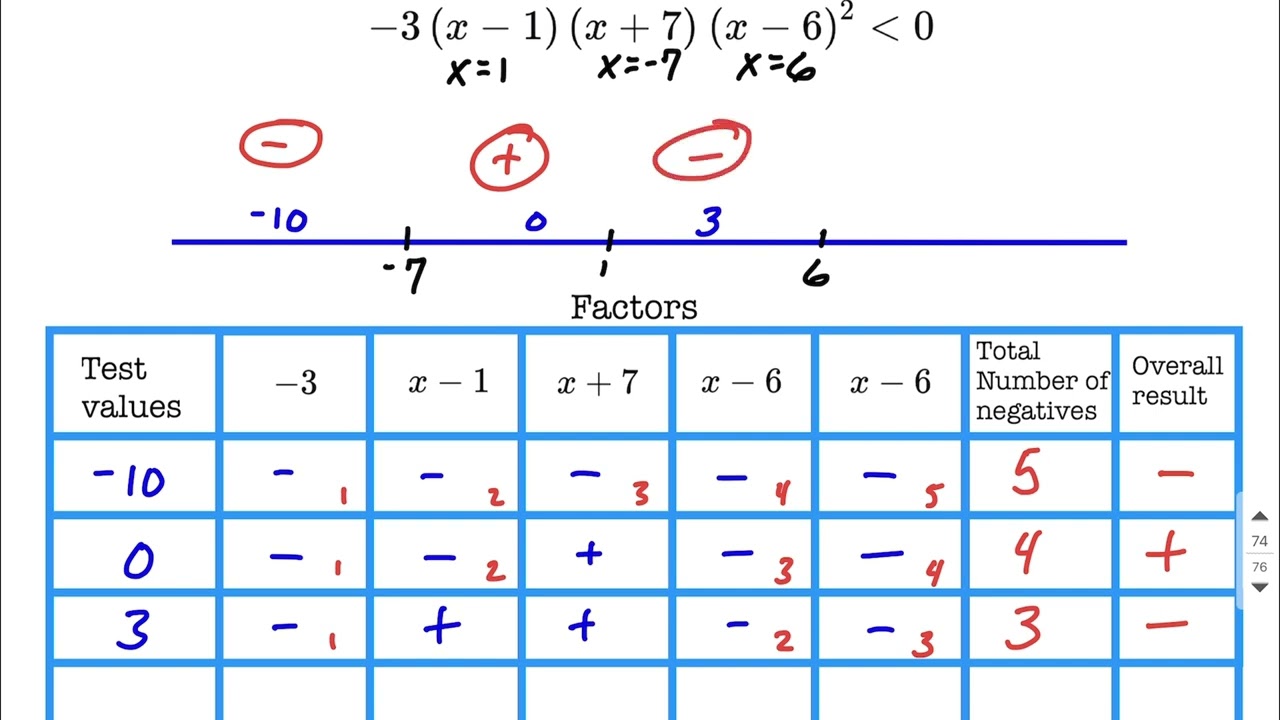
To find our solution sets, we first find which values will make each factor equal zero. These values are then placed in number-line order on a number line. We then choose a value in each section of the number-line to test. To do so, we evaluate the value in each factor and keep track of whether the result is positive or negative. The number of negative factors are then counted. If the result is an even number, then the overall result for that section of the number line is positive while if the result is an odd number, the overall result is negative. This process is repeated for each section of the number line. When we are done, we then look at the inequality sign from the original problem to determine if we are trying to identify the positive sections (greater than zero) or the negative sections (less than zero). The endpoints for our intervals are also discussed as we need to know whether to include the endpoints or not. This is based on whether our inequality was a strict inequality or included an "or equal too" component. After the correct intervals are determined, we write our solution set in proper interval notation.