filmov
tv
Write the equation of a tangent line of a natural logarithmic equation at a value
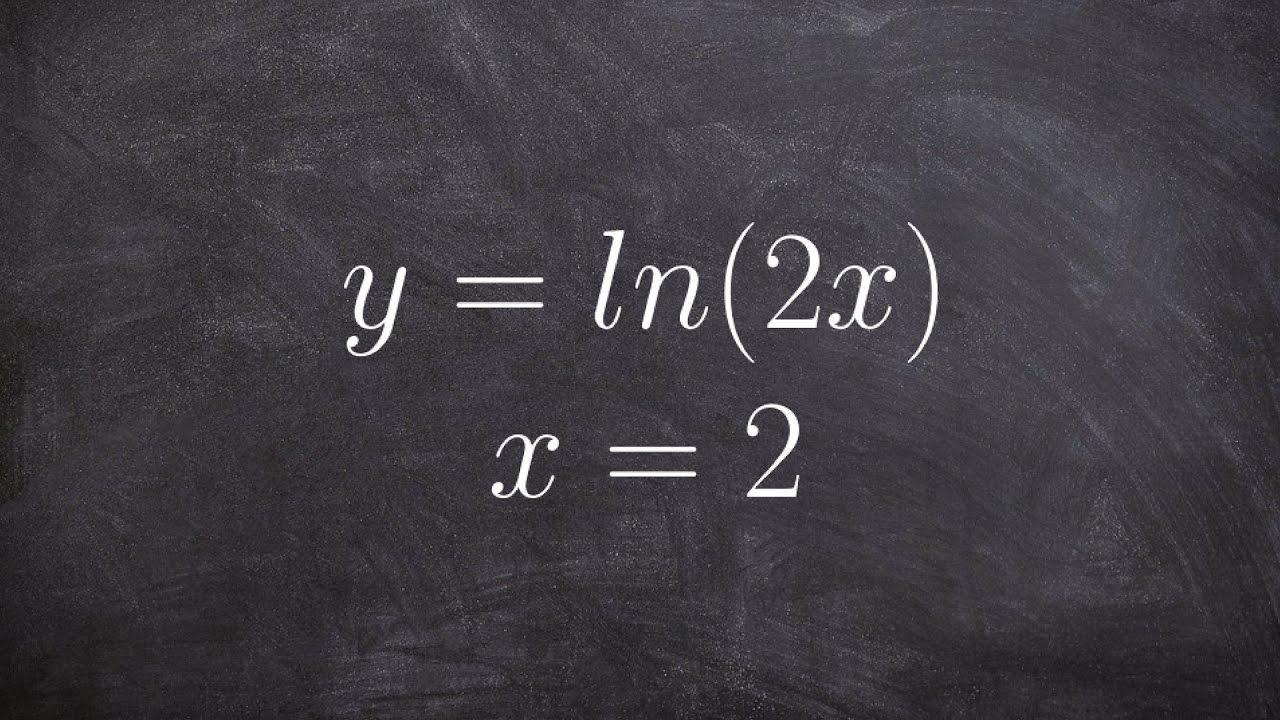
Показать описание
👉 Learn how to find and write the equation of the tangent line of a curve at a given point. The tangent of a curve at a point is a line that touches the circumference of the curve at that point.
To find the equation of the tangent line of a curve at a given point, we start with the point-slope form of the equation of a line given by y - y1 = m(x - x1). The slope of the tangent line at that point is obtained by first differentiating the equation of the curve and then substituting the x-value of the given point into the derivative.
Organized Videos:
✅The Derivative
✅Find the First and Second Derivatives of a Function
✅Find the Differentiability of a Function
✅Find the Derivative of Absolute Value Function
✅Find the Derivative of Exponential and Logarithmic Functions
✅Find the Derivative using Implicit Differentiation
✅Find the Derivative of Inverse Functions
✅Find the Point Where the Tagent Line is Horizontal
✅Write the Equation of the Tangent Line
✅Find the Derivative from a Table
✅Chain Rule Differentiation
✅Product Rule Derivatives
✅Find the Derivative of Trigonometric Functions
✅Find the Derivative using the Power Rule
✅Quotient Rule Derivatives
✅Solve Related Rates Problems
Connect with me:
#derivatives #brianmclogan
To find the equation of the tangent line of a curve at a given point, we start with the point-slope form of the equation of a line given by y - y1 = m(x - x1). The slope of the tangent line at that point is obtained by first differentiating the equation of the curve and then substituting the x-value of the given point into the derivative.
Organized Videos:
✅The Derivative
✅Find the First and Second Derivatives of a Function
✅Find the Differentiability of a Function
✅Find the Derivative of Absolute Value Function
✅Find the Derivative of Exponential and Logarithmic Functions
✅Find the Derivative using Implicit Differentiation
✅Find the Derivative of Inverse Functions
✅Find the Point Where the Tagent Line is Horizontal
✅Write the Equation of the Tangent Line
✅Find the Derivative from a Table
✅Chain Rule Differentiation
✅Product Rule Derivatives
✅Find the Derivative of Trigonometric Functions
✅Find the Derivative using the Power Rule
✅Quotient Rule Derivatives
✅Solve Related Rates Problems
Connect with me:
#derivatives #brianmclogan
Комментарии
 0:08:32
0:08:32
 0:02:09
0:02:09
 0:02:40
0:02:40
 0:10:05
0:10:05
 0:03:25
0:03:25
 0:04:37
0:04:37
 0:14:51
0:14:51
 0:05:07
0:05:07
 0:08:40
0:08:40
 0:08:23
0:08:23
 0:09:35
0:09:35
 0:00:58
0:00:58
 0:24:28
0:24:28
 0:02:19
0:02:19
 0:06:54
0:06:54
 0:03:06
0:03:06
 0:06:49
0:06:49
 0:03:47
0:03:47
 0:02:03
0:02:03
 0:03:50
0:03:50
 0:02:37
0:02:37
 0:01:03
0:01:03
 0:32:05
0:32:05
 0:04:56
0:04:56