filmov
tv
Suppose the three vectors \( \vec{a}, b, \vec{c} \) on a plane satisfy the condition that \( |\v...

Показать описание
Suppose the three vectors \( \vec{a}, b, \vec{c} \) on a plane satisfy the condition that \( |\vec{a}|=|\vec{b}|=|\vec{c}|=|\vec{a}+\vec{b}|=1 ; \vec{c} \) is perpendicular to \( \vec{a} \) and \( \vec{b} \cdot \vec{c}0 \), then for real numbers \( x, y \) the vector \( \vec{p}=x \vec{a}+y \vec{c} \) satisfies the condition \( 0 \leq \vec{p} \cdot \vec{a} \leq 1 \) and \( 0 \leq \vec{p} \cdot \vec{b} \leq 1 \). Find the maximum value of \( \vec{p} \cdot \vec{c} \).
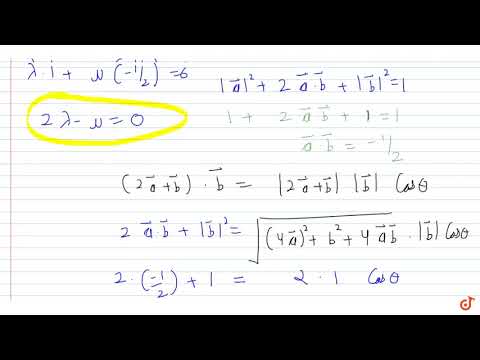 0:08:11
0:08:11
 0:07:57
0:07:57
 0:09:27
0:09:27
 0:11:59
0:11:59
 0:05:58
0:05:58
 0:07:34
0:07:34
 0:07:51
0:07:51
 0:06:56
0:06:56
 0:57:15
0:57:15
 0:05:10
0:05:10
 0:02:00
0:02:00
 0:08:04
0:08:04
 0:04:27
0:04:27
 0:21:42
0:21:42
 0:05:00
0:05:00
 0:26:57
0:26:57
 0:03:33
0:03:33
 0:07:02
0:07:02
 0:00:33
0:00:33
 0:07:34
0:07:34
 0:00:33
0:00:33
 0:11:37
0:11:37
 0:04:27
0:04:27
 0:00:33
0:00:33