filmov
tv
Solve x^2 -(10+5/4 i)x + 21+35/4 I = 0 via completing the square. Complex number coefficients
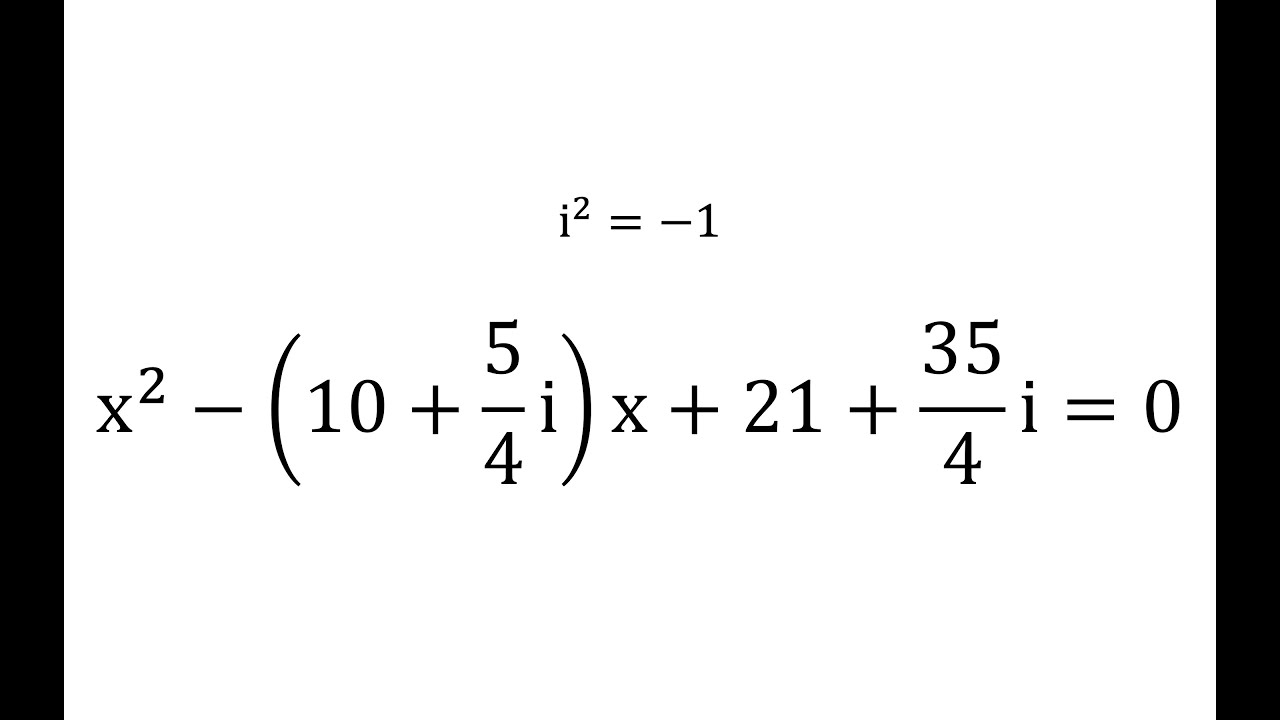
Показать описание
Didn't all of you think that complex roots/zeroes occurred in conjugate pairs?! Well I have an exception OR do I? A careful recollection of the math theorem about polynomials having complex number roots existing as conjugate pairs solves this dilemma.
Completing the square along with solving the quartic equation that results from a+bi=√(231/64-20/8 i) after squaring are the crucial steps along with what appears to be an exception to the rational zero theorem at first glance! Gopal Menon
Prime Math Lovers, hyperbolically, did a video on unlocking the secrets of polynomial equations and quadratic equations. Yeah right :)
a^4 -231/64 a^2 - 25/16 = 0 note that the constant term 25/16 = 2 times 25/32
Completing the square along with solving the quartic equation that results from a+bi=√(231/64-20/8 i) after squaring are the crucial steps along with what appears to be an exception to the rational zero theorem at first glance! Gopal Menon
Prime Math Lovers, hyperbolically, did a video on unlocking the secrets of polynomial equations and quadratic equations. Yeah right :)
a^4 -231/64 a^2 - 25/16 = 0 note that the constant term 25/16 = 2 times 25/32