filmov
tv
Solving a system of linear equations | Wild Linear Algebra A 13 | NJ Wildberger

Показать описание
This is the 13th lecture in this course on Linear Algebra. Here we start studying general systems of linear equations, matrix forms for such a system, row reduction, elementary row operations and row echelon forms.
This course is given by Assoc Prof N J Wildberger of UNSW, who also has other YouTube series, including WildTrig, MathFoundations and Algebraic Topology.
CONTENT SUMMARY: pg 1: @00:08 How to solve general systems of equations; Chinese "Nine chapters of the mathematical art'/C.F.Gauss; row reduction;
pg 2: @03:04 General set_up: m equations in n variables; Matrix formulation; matrix of coefficients;
pg 3: @05:50 Defining the product of a matrix by a column vector; 2 propositions used throughout the remainder of course; matrix formulation of basic system of equations;
pg 4: @09:07 return to original example; Linear transformation;
pg 5: @10:49 a 3rd way of thinking about our system of linear equations; vector formulation; example;
pg 6: @14:12 example: row reduction (working with equations);
pg 7: @24:48 example: row reduction (working with matrices); row echelon form mentioned; reduced row echelon form; setting a variable to a parameter;
pg 8: @30:17 Terminology; augmented matrix, leading entry, leading column, row echelon form;
pg 9: @32:07 examples; solution strategy;
pg 10: @35:36 elementary row operations; operations are invertible (can be undone); algorithm for row reducing a matrix;
pg 11: @38:11 algorithm for row reducing a matrix; pivot entry;
pg 12: @43:41 example; row reducing a matrix per algorithm;
pg 13: @47:38 exercises 13.(1:2);
pg 14: @48:02 exercise 13.3; (THANKS to EmptySpaceEnterprise)
Video Chapters:
00:00 Introduction
3:02 General setup: m equations in n variables
5:50 Product of matrix by vector
14:12 Equations and row reduction
30:17 Terminology echelon forms
30:36 Elementary row operations
38:11 Row reducing algorithm
43:41 Row reduction exercise
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
This course is given by Assoc Prof N J Wildberger of UNSW, who also has other YouTube series, including WildTrig, MathFoundations and Algebraic Topology.
CONTENT SUMMARY: pg 1: @00:08 How to solve general systems of equations; Chinese "Nine chapters of the mathematical art'/C.F.Gauss; row reduction;
pg 2: @03:04 General set_up: m equations in n variables; Matrix formulation; matrix of coefficients;
pg 3: @05:50 Defining the product of a matrix by a column vector; 2 propositions used throughout the remainder of course; matrix formulation of basic system of equations;
pg 4: @09:07 return to original example; Linear transformation;
pg 5: @10:49 a 3rd way of thinking about our system of linear equations; vector formulation; example;
pg 6: @14:12 example: row reduction (working with equations);
pg 7: @24:48 example: row reduction (working with matrices); row echelon form mentioned; reduced row echelon form; setting a variable to a parameter;
pg 8: @30:17 Terminology; augmented matrix, leading entry, leading column, row echelon form;
pg 9: @32:07 examples; solution strategy;
pg 10: @35:36 elementary row operations; operations are invertible (can be undone); algorithm for row reducing a matrix;
pg 11: @38:11 algorithm for row reducing a matrix; pivot entry;
pg 12: @43:41 example; row reducing a matrix per algorithm;
pg 13: @47:38 exercises 13.(1:2);
pg 14: @48:02 exercise 13.3; (THANKS to EmptySpaceEnterprise)
Video Chapters:
00:00 Introduction
3:02 General setup: m equations in n variables
5:50 Product of matrix by vector
14:12 Equations and row reduction
30:17 Terminology echelon forms
30:36 Elementary row operations
38:11 Row reducing algorithm
43:41 Row reduction exercise
************************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
Комментарии
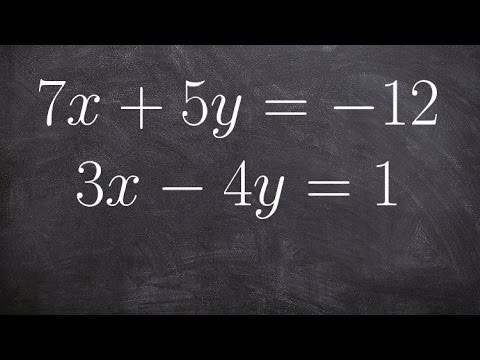 0:04:34
0:04:34
 0:18:40
0:18:40
 0:10:21
0:10:21
 0:10:52
0:10:52
 0:10:27
0:10:27
 0:05:59
0:05:59
 0:05:15
0:05:15
 0:09:21
0:09:21
 0:15:34
0:15:34
 0:12:28
0:12:28
 0:12:44
0:12:44
 0:12:16
0:12:16
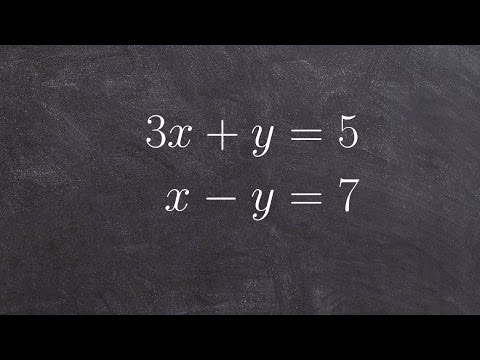 0:05:22
0:05:22
 0:08:30
0:08:30
 0:09:55
0:09:55
 0:10:47
0:10:47
 0:32:05
0:32:05
 0:13:37
0:13:37
 0:18:47
0:18:47
 0:12:44
0:12:44
 0:19:44
0:19:44
 0:02:55
0:02:55
 0:16:25
0:16:25
 0:06:28
0:06:28