11/12.3 Entropy and the Second Law of Thermodynamics | General Physics

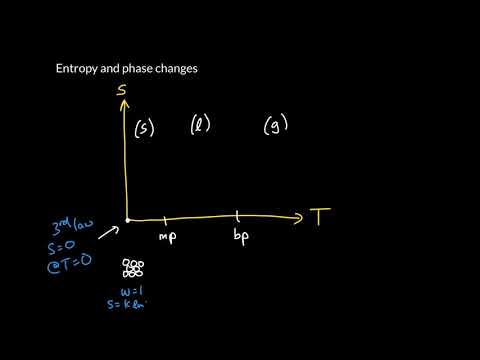
Chad provides a lesson on Entropy and the Second Law of Thermodynamics. The lesson begins with a conceptual description of entropy as a measure of disorder. The Second Law of Thermodynamics is then presented showing that the entropy of the universe increases for a spontaneous process. A more formal and mathematical definition for entropy change follows along with the presentation and derivation of equations for calculating entropy for an isothermal expansion or compression as well as the demonstration that the entropy change for an adiabatic process is zero. Chad also shows how to calculate the entropy change associated with heating or cooling and solves an example calculation.

Chad next presents the mathematical relationship between entropy and the number of microstates.
S=kBlnW
Chad shows that a system for which only 1 microstate exists will have zero entropy, and then as the number of microstates increases, so too does the entropy. Systems that have more disorder tend to also have more microstates explaining why they also have more entropy.

The lesson is concluded with a discussion of heat engines and thermal efficiency. An expression for the work performed by a heat engine is presented along with an expression for calculating the thermal efficiency of a heat engine. A Carnot engine is then described as an engine with the highest possible thermal efficiency. The four steps of the Carnot Cycle are then described:
1. Isothermal Expansion
2. Adiabatic Expansion
3. Isothermal Compression
4. Adiabatic Compression
It is shown how the thermal efficiency of a Carnot engine is dependent only upon the temperature of the hot reservoir (heat sink) and cold reservoir (cold sink), and that the thermal efficiency can never actually reach 100%.

00:00 Lesson Introduction
00:51 Entropy and Disorder
01:23 Second Law of Thermodynamics
05:01 Entropy Change Definition and Calculations
07:13 How to Calculate Delta S for Heating and Cooling
15:30 Entropy and Microstates
20:40 Heat Engines and Thermal Efficiency
24:38 The Carnot Cycle and Thermal Efficiency

[KL-jtnx]

And he's back with another video!

[MrFeras_]

Dr. Chad 10:56 in this question the final temperature should be 60 C ??

[SakeenaManzoor-uy]

24 :38 is the time in the video sir the question is if we have an adiabatic compression or expansion then we only insulate the bottom of cylinder in which a gas is filled?? Sir do we also insulate our container in which gas is filled in order to prevent the exchange of heat?? Because as in adiabatic compression you said that gas become hot if we have insulated container then how we make the gas hot by compressed it??

[SakeenaManzoor-uy]

Sir can you give me an example of ehtropy except that of dyes i don't understand it.😢

[yigitcan]

Professor, I have a question here . 2nd law states that _Energy has a quality as well as quantity_ .Here *quality* refers to what? I do not understand the meaning of quality in this sentence?Is there low quality energy or high quality energy etc?

[walteranonmitty]

So 'gravity' is simply an entropic spontaneous process.

Bingo!

[walteranonmitty]

Carno cycle? Karno cycle? You need to write these terms down please LEGIBLY