filmov
tv
The integral of e^(-x^2) & the error function

Показать описание
The Error Function is the integral of e^(-x^2) and is closely related to the Gaussian integral. This is a non-elementary function (or you can call it an advanced function).
Integrating e^(-x^2) The Gaussian Integral
The integral of e^(-x^2) & the error function
Integral of e^(x^2) & the Imaginary Error Function
The Gaussian Integral! Integral of e^(-x^2) from 0 to infinity via polar coordinates
Gaussian Integral [Int{e^-x^2} from -inf to inf]
Integrating Exponential Functions By Substitution - Antiderivatives - Calculus
It 'Cannot' Be Done (Integrals)
how Laplace solved the Gaussian integral
The Gaussian Integral
improper integral of x*e^(-x^2) from -inf to +inf
The Gaussian Integral // Solved Using Polar Coordinates
Learn how to integrate e^(2x)
Integral of (x^2)*(e^x)
G1. Integral gaussiana: demostración de Laplace (Integral doble, impropia, cambio de variable)
Integral of (2x)*e^(x^2) (substitution)
Integral of (2x^2+1)e^(x^2) (by parts)
PARTIELLE INTEGRATION e Funktion – Beispiel x^2*e^x, Grenzen, doppelt, zweimal anwenden
Integral of x^2e^-x^2 from 0 to infinity. 💪
Integration by parts x^2 e^x
Find the indefinite integral for x^2 e^(-x) dx. Integration by Parts
Ex 2: Improper Integral - Infinite Interval (-inf, constant)
The Improper Integral of e^(-x) from 0 to Infinity
integral of sqrt(x)*e^(-x) from 0 to inf
Evaluate the integral by reversing the order of integration
Комментарии
 0:01:30
0:01:30
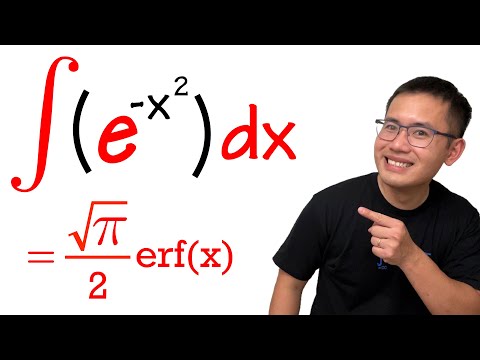 0:12:52
0:12:52
 0:08:23
0:08:23
 0:08:15
0:08:15
 0:14:03
0:14:03
 0:11:16
0:11:16
 0:03:11
0:03:11
 0:15:01
0:15:01
 0:10:09
0:10:09
 0:05:20
0:05:20
 0:07:52
0:07:52
 0:01:55
0:01:55
 0:03:58
0:03:58
 0:14:51
0:14:51
 0:00:43
0:00:43
 0:01:47
0:01:47
 0:09:23
0:09:23
 0:03:59
0:03:59
 0:05:12
0:05:12
 0:04:07
0:04:07
 0:04:57
0:04:57
 0:03:28
0:03:28
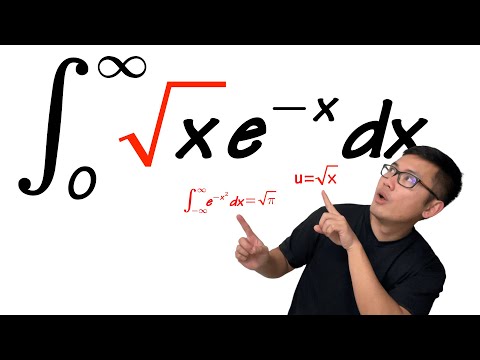 0:10:18
0:10:18
 0:08:15
0:08:15