filmov
tv
A nice #shorts trick for complex numbers.
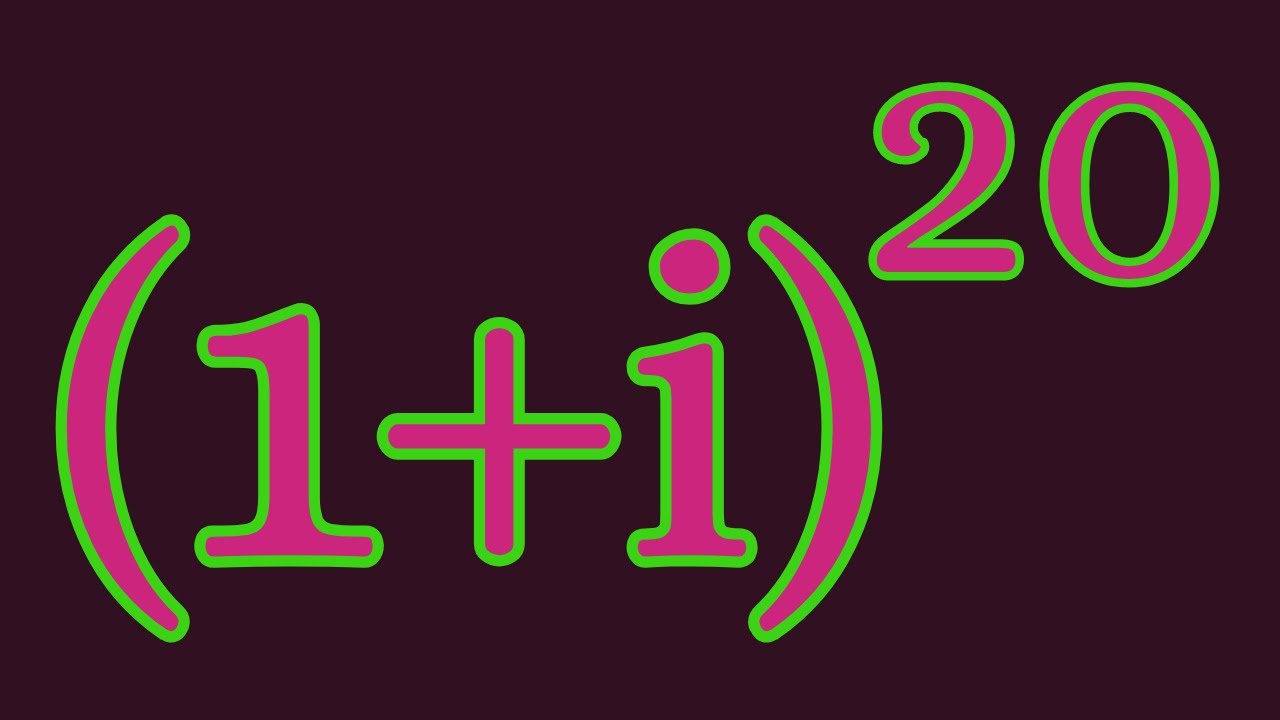
Показать описание
#shorts
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
EASY Rubber-Band Magic Trick Revealed! #shorts
Creative Trick with a Bolt, Wire, and Bracket! #shorts #tricks
DAS beeindruckt DEINE FREUNDE! 😍 #shorts #tiktok #diy #tricks
Nice 3 digit multiplication short trick#trending#maths#mathematics#shorts#education#youtubeshorts 🔥🔥...
Vertrau mir: Zollstocktrick für die Baustelle #handwerk #tricks #shorts #tips #howto
Kleber in den Haaren?!😱 #fakten #tricks #gefährlich #shorts #deutsch
Fireon Water 😱|ScienceExperiment | #science😱 #shorts#short #magic #trick #viralshorts #magic
CAN YOU DO IT? 😳🤔🤣 VIRAL TIKTOK HAIR TIE TRICK TUTORIAL? 👀 #shorts #viral #trend #tutorial...
part.2 easy trick to tighten bolt #hacks #tips #tricks #diy #lifehacks #shorts #shortsfeed #trend
CAN YOU DO IT? 😳🤔🤣 VIRAL TIKTOK HAIR TIE TRICK TUTORIAL? 👀 #shorts #viral #trend #tutorial...
Danish Gambit at its Best | Chess Opening Tricks to WIN Fast #shorts
CAN YOU DO IT? 😳🤔🤣 VIRAL TIKTOK HAIR TIE TRICK TUTORIAL? 👀 #shorts #viral #trend #tutorial...
CAN YOU DO IT? 😳🤔🤣 VIRAL TIKTOK HAIR TIE TRICK TUTORIAL? 👀 #shorts #viral #trend #tutorial...
Let’s make a PORTAL 🌀 #shorts
Der Trick ist crazy 🤫 #shorts
Nice multiplication short trick#trending#mathstricks#maths#shorts#education#youtubeshorts#multiply🔥🔥...
Checkmate in just 4 moves! The Scholar's Mate #Shorts
How To Win Chess in 2 Moves #Shorts
Quick Aerial Hammock Trick for Beginners - Aerial Yoga Trick #shorts
crazy mobile videography trick 😱#shorts #videography #tricks
this hair trick actually works😭👍
Lerne diesen Trick #fußball #tricks #tutorial #shorts
Learn How To Hold A Handstand - Fast Trick #Shorts
NASTY Combo 🔥
Комментарии
 0:00:30
0:00:30
 0:00:14
0:00:14
 0:00:31
0:00:31
 0:00:33
0:00:33
 0:00:46
0:00:46
 0:00:30
0:00:30
 0:00:23
0:00:23
 0:00:08
0:00:08
 0:00:18
0:00:18
 0:00:08
0:00:08
 0:00:59
0:00:59
 0:00:13
0:00:13
 0:00:15
0:00:15
 0:00:19
0:00:19
 0:00:17
0:00:17
 0:00:29
0:00:29
 0:00:28
0:00:28
 0:00:31
0:00:31
 0:00:40
0:00:40
 0:00:13
0:00:13
 0:00:15
0:00:15
 0:00:15
0:00:15
 0:00:35
0:00:35
 0:00:17
0:00:17