filmov
tv
Finding the nth term of 3,5,9,15,...

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #SequencesAndSeries
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #SequencesAndSeries
EXPLORE 😎:
PLAYLISTS 🎵 :
GCSE Maths - How to Write Expressions for the nth term of Arithmetic Sequences #55
How To Find The Nth Term of an Arithmetic Sequence
Find the nth term in a sequence
Finding the Nth Term
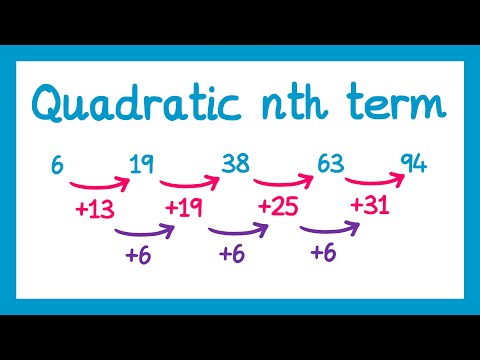
Finding the nth term of a Quadratic Sequence - GCSE Higher Maths
Quadratic Sequences: nth Term | Algebra | Maths | FuseSchool
How to Find the Nth Term Equation | Fun Math | JusticeTheTutor #math #maths #shorts
Learn How to Find the nth Term of an Arithmetic Sequence Example with 2, 6, 10, 14, ...
04 Sequence And Series|| Sum of the sequence and series grade 12 || Class 12 mathematics #NEB #maths
Nth Term In Seconds!!
How do you find the formula for the nth term of an arithmetic sequence
find the nth term of A.P 3,7,11,15........... 1.6M
Finding the Nth Rule of Arithmetic Sequence | Explain in Detailed |
Find The Nth Term Of a Linear Sequence
Finding the Nth Term of an Arithmetic Sequence | Grade 10 Math
The Maths Prof: Sequences nth Term (part 1)
Nth Term of Linear Sequences | GCSE Maths 2025
How to find nth term SIMPLE #shorts #maths
The Nth Term of Quadratic Sequences
How to Find the Nth Term of an AP Series / Finding the nth term of an AP Series Using Formula
Finding the first 5 terms of the sequence given the nth term
Finding the Nth Term of a Linear Sequence Part 1
How to find the nth term of a linear sequence
FINDING THE nth TERM IN ARITHMETIC SEQUENCE
Комментарии
 0:06:15
0:06:15
 0:06:13
0:06:13
 0:03:09
0:03:09
 0:05:30
0:05:30
 0:05:44
0:05:44
 0:03:21
0:03:21
 0:00:33
0:00:33
 0:01:54
0:01:54
 0:09:49
0:09:49
 0:00:08
0:00:08
 0:04:08
0:04:08
 0:00:24
0:00:24
 0:21:09
0:21:09
 0:04:28
0:04:28
 0:10:14
0:10:14
 0:08:09
0:08:09
 0:00:59
0:00:59
 0:00:14
0:00:14
 0:09:32
0:09:32
 0:02:45
0:02:45
 0:16:07
0:16:07
 0:03:58
0:03:58
 0:00:53
0:00:53
 0:06:20
0:06:20